ABCD is a rhombus in which altitude from point D to the side AB bisects AB. The angles of the rhombus are :
150∘,30∘,150∘,30∘
135∘,45∘,135∘,45∘
1161∘3,632∘3,1161∘3,622∘3
120∘,60∘,120∘,60∘
The correct Answer is:D
To find the angles of the rhombus ABCD where the altitude from point D to side AB bisects AB, we can follow these steps:
1. Understanding the Properties of a Rhombus:
- A rhombus is a type of quadrilateral where all four sides are of equal length.
- The diagonals of a rhombus bisect each other at right angles.
2. Drawing the Diagram:
- Draw rhombus ABCD.
- Mark points A, B, C, and D.
- Drop a perpendicular from point D to line AB, and let it meet AB at point O (the midpoint of AB).
3. Identifying Triangles:
- We can form two right triangles, triangle ADO and triangle BDO.
- Since DO is perpendicular to AB, angle ADO and angle BDO are both 90 degrees.
4. Using Congruence:
- Since AO = BO (because O is the midpoint of AB) and AD = DB (as all sides of a rhombus are equal), we can say that triangles ADO and BDO are congruent by the Side-Angle-Side (SAS) criterion.
5. Finding Angles:
- Since triangles ADO and BDO are congruent, we have:
- Angle ADO = Angle BDO = 90 degrees
- AD = DB
- This means that both triangles ADO and BDO are isosceles right triangles.
6. Calculating Angles A and C:
- In triangle ADO, since it is an isosceles right triangle, the angles A and O are equal.
- Therefore, angle A = angle O = 30 degrees (since the total angle in triangle ADO is 180 degrees, and one angle is 90 degrees).
7. Calculating Angles B and D:
- Since angle A + angle B + angle C + angle D = 360 degrees and angles A and C are equal, we can derive:
- Angle A + Angle C = 60 degrees (from the isosceles triangle property).
- Therefore, angle B + angle D = 360 - 60 = 300 degrees.
- Since angle B = angle D, we have 2x = 300 degrees, leading to x = 150 degrees.
8. Final Angles:
- Thus, the angles of rhombus ABCD are:
- Angle A = 30 degrees
- Angle B = 150 degrees
- Angle C = 30 degrees
- Angle D = 150 degrees
Summary of Angles:
- Angle A = 30 degrees
- Angle B = 150 degrees
- Angle C = 30 degrees
- Angle D = 150 degrees
- A rhombus is a type of quadrilateral where all four sides are of equal length.
- The diagonals of a rhombus bisect each other at right angles.
- Draw rhombus ABCD.
- Mark points A, B, C, and D.
- Drop a perpendicular from point D to line AB, and let it meet AB at point O (the midpoint of AB).
- We can form two right triangles, triangle ADO and triangle BDO.
- Since DO is perpendicular to AB, angle ADO and angle BDO are both 90 degrees.
- Since AO = BO (because O is the midpoint of AB) and AD = DB (as all sides of a rhombus are equal), we can say that triangles ADO and BDO are congruent by the Side-Angle-Side (SAS) criterion.
- Since triangles ADO and BDO are congruent, we have:
- Angle ADO = Angle BDO = 90 degrees
- AD = DB
- This means that both triangles ADO and BDO are isosceles right triangles.
- In triangle ADO, since it is an isosceles right triangle, the angles A and O are equal.
- Therefore, angle A = angle O = 30 degrees (since the total angle in triangle ADO is 180 degrees, and one angle is 90 degrees).
- Since angle A + angle B + angle C + angle D = 360 degrees and angles A and C are equal, we can derive:
- Angle A + Angle C = 60 degrees (from the isosceles triangle property).
- Therefore, angle B + angle D = 360 - 60 = 300 degrees.
- Since angle B = angle D, we have 2x = 300 degrees, leading to x = 150 degrees.
- Thus, the angles of rhombus ABCD are:
- Angle A = 30 degrees
- Angle B = 150 degrees
- Angle C = 30 degrees
- Angle D = 150 degrees
- Angle A = 30 degrees
- Angle B = 150 degrees
- Angle C = 30 degrees
- Angle D = 150 degrees
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - QUESTION BANK - 23
20 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
10 Videos
- PROBABILITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -29
10 Videos
Similar Questions
Knowledge Check
If ABCD is a rhombus, then
AAC2+BD2=6AB2BAC2+BD2=5AB2CAC2+BD2=4AB2DAC2+BD2=3AB2If ABCD is a rhombus, then
AAC2+BD2=AB2BAC2+BD2=2AB2CAC2+BD2=4AB2DAC2+BD2=3AB2If ABCD is a rhombus, then :
AAC2+BD2=4AB2BAC2+BD2=AB2CAC2+BD2=2AB2D2(AC2+BD2)=3AB2
Diagonal AC of a rhombus ABCD is a equal to one of its sides BC. Find all the angles of the rhombus.
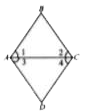
View SolutionABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then Δ ABD is equilateral.
View SolutionOne of the diagonals of a rhombus is equal to one of its sides. Find the angles of the rhombus.
View SolutionIf ABCD is a rhombus, then :
View SolutionABCD is a rhombus in which ∠C=60∘then AC:BD=.
View Solution
