ABCD is a trapezium in which AB∣∣DC and its diagonals intersect each other at point ‘O’. Show that AOBO=CODO.Solution in Telugu
Step by step video & image solution for ABCD is a trapezium in which AB|\|DC and its diagonals intersect each other at point ‘O’. Show that (AO)/(BO)=(CO)/(DO). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO show that ABCD is a trapezium.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other as the point O. Show that AOBO=CODO.
View SolutionABCDಯು ಒಂದು ತ್ರಾಪಿಜ್ಯ ಇದರಲ್ಲಿ AB || DC ಮತ್ತು ಕರ್ಣಗಳು ಪರಸ್ಪರ O ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ. ಆದರೆ AOBO=CODO ಎಂದು ತೋರಿಸಿ.
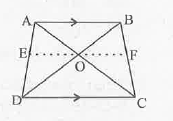
View SolutionABCD is a trapezium in which AB∣∣DC and its diagonals intersect each other at the point O. Show that AOBO=CODO
View SolutionABCD is a trapezium in which AB∣∣DC and its diagonals intersects each other at the point O. Show that AOBO=CODO.
View SolutionThe diagonals of a quadrilateral ABCD intersects each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionABCD is a trapezium in which AB II DC and its diagonals intersect each other at the point O. show that AOBO=CODO .
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point o Such that AOBO=CODO , show that ABCD is trapezium.
View Solution