ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
Video Solution
Text Solution
GIVEN A trapezium ABCD in which AB∣∣CD and its diagonals AC and BD intersect at O.
TO PROVE AOOC=BOOD
CONSTRUCTION Through O, draw EO∣∣AB, meetng AD at E.
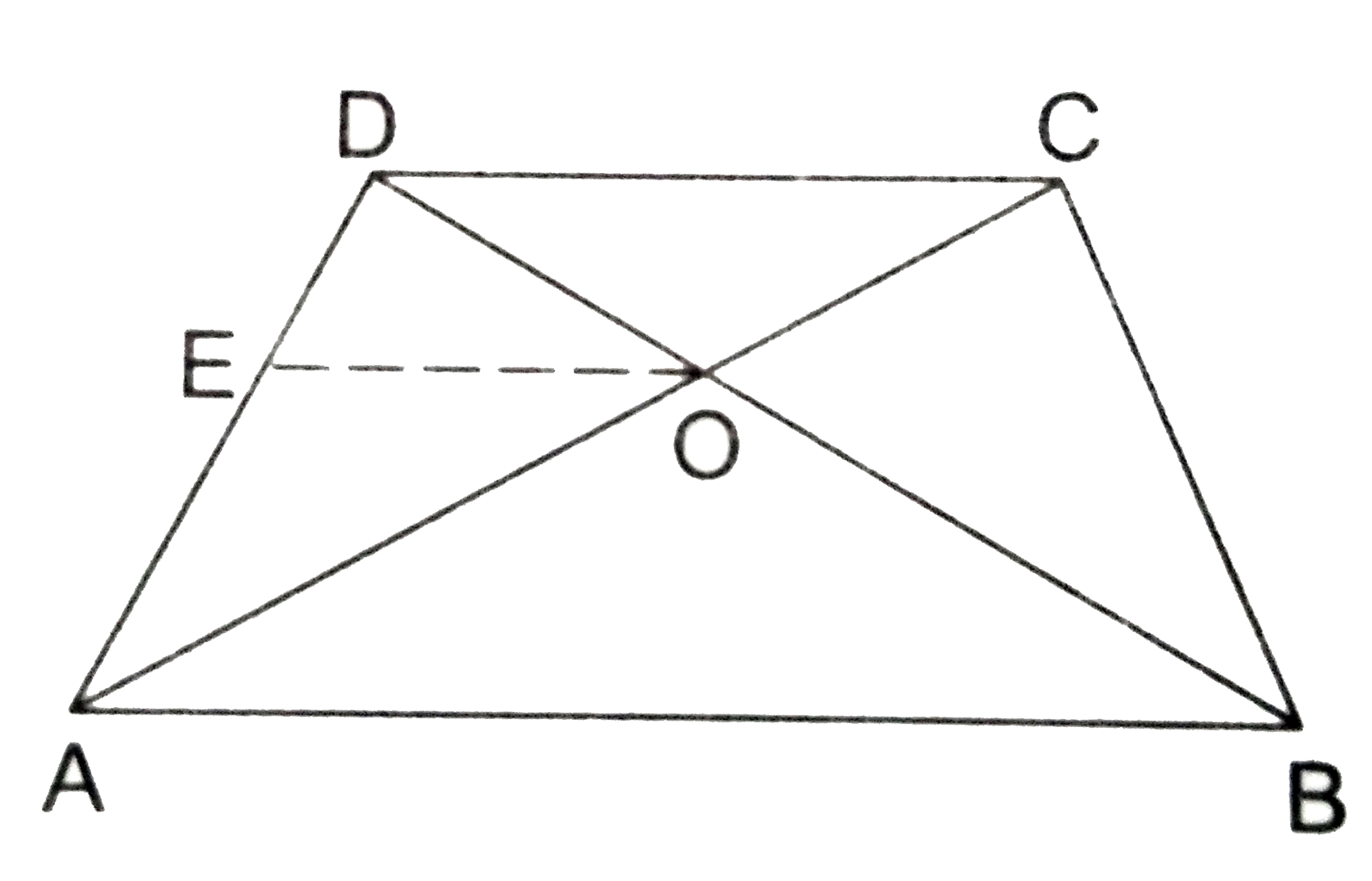
PROOF In ΔADC,EO∣∣DC[∴EO||AB||DC]
∴AEED=AOOC .....(i) [ by Thale's theorem]
In ΔDBA,EO∣∣AB.
∴DEEADOOB [ by Thale's theorem]
⇒nAEED=BDOD .....(ii)
From (i) and (ii), we get
AOOC=BOOD
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
ABCD is a regular trapezium in which AD∣∣BC Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
A−8,9B8,−9C−8,−9D8,9ABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C1:4D4:1ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4B1:2C4:1D2:1
Diagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View Solution(A) Complete any one out of two activities :
In Quadilateral ABCD , diagonals AC and BD intersect each other at point E
If AEEC=BEED then complete the following activity to prove
ABCD is a trapezium
View SolutionIn trapezium AC and BD intersect each other at point P. Then prove that A(ΔABP)A(ΔCPD)=AB2CD2.
View SolutionDiagonals AC and BD of a trapezium ABCD with ABCD intersect each where at O. Prove that ar (AOD)=ar(BOC).
View Solution
