ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
To prove that AEED=BFFC in trapezium ABCD where AB∥DC and EF∥AB, we can follow these steps:
Step 1: Identify the triangles
We have trapezium ABCD with AB∥DC. Points E and F are located on sides AD and BC respectively, such that EF∥AB.
Step 2: Apply the Basic Proportionality Theorem
Since EF is parallel to AB, by the Basic Proportionality Theorem (also known as Thales' theorem), we can conclude that:
AEED=AFFB
Let's denote this as Equation (1).
Step 3: Consider triangle ADC
In triangle ADC, since EF∥DC, we can apply the Basic Proportionality Theorem again:
AEED=AGGC
where G is the intersection point of line EF with line AC. Let's denote this as Equation (2).
Step 4: Consider triangle ABC
Now, in triangle ABC, since EF∥AB, we can apply the Basic Proportionality Theorem:
BFFC=AGGC
Let's denote this as Equation (3).
Step 5: Relate the equations
From Equations (2) and (3), we have:
AEED=AGGC(from Equation 2)
BFFC=AGGC(from Equation 3)
Since both ratios equal AGGC, we can equate them:
AEED=BFFC
Conclusion
Thus, we have shown that:
AEED=BFFC
Hence proved.
---
We have trapezium ABCD with AB∥DC. Points E and F are located on sides AD and BC respectively, such that EF∥AB.
Since EF is parallel to AB, by the Basic Proportionality Theorem (also known as Thales' theorem), we can conclude that:
AEED=AFFB
Let's denote this as Equation (1).
In triangle ADC, since EF∥DC, we can apply the Basic Proportionality Theorem again:
AEED=AGGC
where G is the intersection point of line EF with line AC. Let's denote this as Equation (2).
Now, in triangle ABC, since EF∥AB, we can apply the Basic Proportionality Theorem:
BFFC=AGGC
Let's denote this as Equation (3).
From Equations (2) and (3), we have:
AEED=AGGC(from Equation 2)
BFFC=AGGC(from Equation 3)
Since both ratios equal AGGC, we can equate them:
AEED=BFFC
Thus, we have shown that:
AEED=BFFC
Hence proved.
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
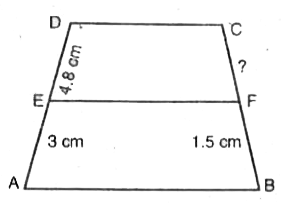 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of these - Question 2 - Select One
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2 - Question 3 - Select One
In a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
ABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).
 View Solution
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View SolutionD and E are points on the sides AB and AC respectively such that AB=3.6 cm and AD=1.4 AC=7.2 and AE=1.8. Show that DE is parallel to BC
View Solution


