ABCD is an isosceles trapezium . . AE and BF are the perpendicular drawn to CD. The congruence property used to prove the congurence of triangles AED and BFC is ______
A
RHS
B
SAS
C
SSS
D
ASA
Video Solution
Text Solution
The correct Answer is:A
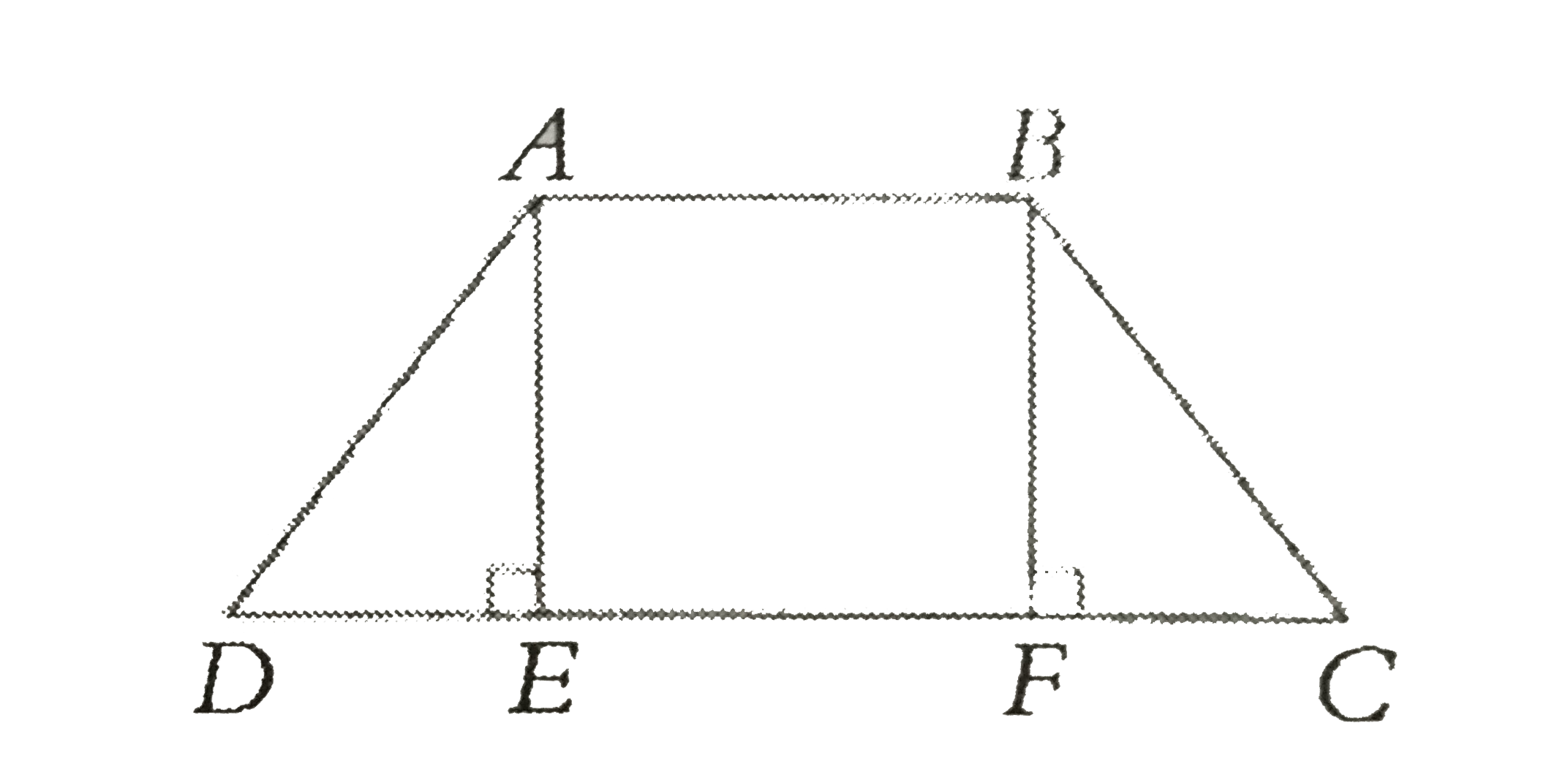
In
AD=BC
AE=BF= Height of the trapezium.
By RHS, are congruent.
Option (a) follows.
Hence, the correct option is (a).
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-3
19 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-1
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-1
24 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check
ABCD is an isosceles trapezium . ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. AE and BF are the perpendicular drawn to CD. The congruence property used to prove the congurence of triangles AED and BFC is ______
ARHSBSASCSSSDASAABCD is an isosceles trapezium in which ¯¯¯¯¯¯AB||¯¯¯¯¯¯CDand∠A=57∘ . Find the value of ∠C+∠D.
A112∘B123∘C246∘D303∘The parallel sides of a trapezium ABCD are 16 cm. AF and BE and are the perpendiculars drawn to ¯¯¯¯¯¯DC. Find the total area of the triangle ADF and BCE (in cm2).
A36B24C30D28
ΔABC is an isosceles triangle. AB = AC and BD is perpendicular on AC from vertex B, then BD2−CD2 is equal to-
View SolutionIn a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View Solution
In the figure above ,AB is the perpendicular bisector of CD. Which of the following axioms best proves the congurence of ΔABCandΔABD ?
View SolutionIf ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =
View SolutionIn ΔPQRandΔABC, ∠Q=∠B=90∘,PQ=AB,andQR=BC. Which of the following property can be used to prove the congruence of ΔPQR and ΔABC ?
View Solution
