A,B,E are 3 points of the circumference of a circle of radius 1. If angle AEB = . Then length of AB is
To find the length of segment AB in a circle with radius 1, given that angle AEB is π/4, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O and radius 1. Points A, B, and E lie on the circumference of the circle, and we know that angle AEB = π/4.
Step 2: Relate the Angle AEB to the Central Angle
According to the inscribed angle theorem, the angle subtended at the center (angle AOB) is twice the angle subtended at any point on the circumference (angle AEB). Therefore:
∠AOB=2×∠AEB=2×π4=π2
Step 3: Visualize the Triangle
Now, we can visualize triangle AOB. Since angle AOB is π/2 (90 degrees), triangle AOB is a right triangle.
Step 4: Apply the Pythagorean Theorem
In triangle AOB:
- OA = 1 (radius)
- OB = 1 (radius)
- AB is the hypotenuse.
By the Pythagorean theorem:
AB2=OA2+OB2
Substituting the values:
AB2=12+12=1+1=2
Thus,
AB=√2
Conclusion
The length of segment AB is √2.
---
We have a circle with center O and radius 1. Points A, B, and E lie on the circumference of the circle, and we know that angle AEB = π/4.
According to the inscribed angle theorem, the angle subtended at the center (angle AOB) is twice the angle subtended at any point on the circumference (angle AEB). Therefore:
∠AOB=2×∠AEB=2×π4=π2
Now, we can visualize triangle AOB. Since angle AOB is π/2 (90 degrees), triangle AOB is a right triangle.
In triangle AOB:
- OA = 1 (radius)
- OB = 1 (radius)
- AB is the hypotenuse.
AB2=OA2+OB2
Substituting the values:
AB2=12+12=1+1=2
Thus,
AB=√2
The length of segment AB is √2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the circumference of a circle of radius 10 cm. (Takeπ=3.14.]
A72.8cmB62.8cmC82.8cmD92.8cmLet A, B, C be three points on a circle of radius 1 such that ∠ACB=π4. Then the length of the side AB is
A√3B43C3√2D√2A point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
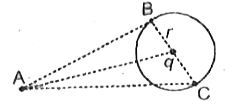 AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0
AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0
Ratio of circumference of a circle to its radius is always 2π:I.
View SolutionA,B,C and D are 4 points on the circumference of the circle and O is the centre of circle ∠OBD−∠CBD=∠BDC−∠ODB find ∠A
View SolutionA,B,C are three points on the circumference of a circle and if ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=5√2 cm and ∠BAC=90∘, find the radius.
View SolutionA,B,C are three points on the circumference of a circle and if ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=5√2 cm and ∠BAC=90∘, find the radius.
View SolutionIn the given diagram, AB is the diameter of the given circle with centre O. C and D are points on the circumference of the circle. If ∠ABD=35∘and∠CDB=15∘, then ∠ CBD equals.
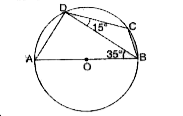
View Solution
