All the point (a, y) in the plane satisfying the equation x2+2xsin(xy)+1=0 lie on -
A
a pair of straight lines
B
a family of hyperbolas
C
a parabola
D
an ellipse
Text Solution
The correct Answer is:A
x2+2xsin(xy)+1=0
2sin(xy)=−(x+1x)
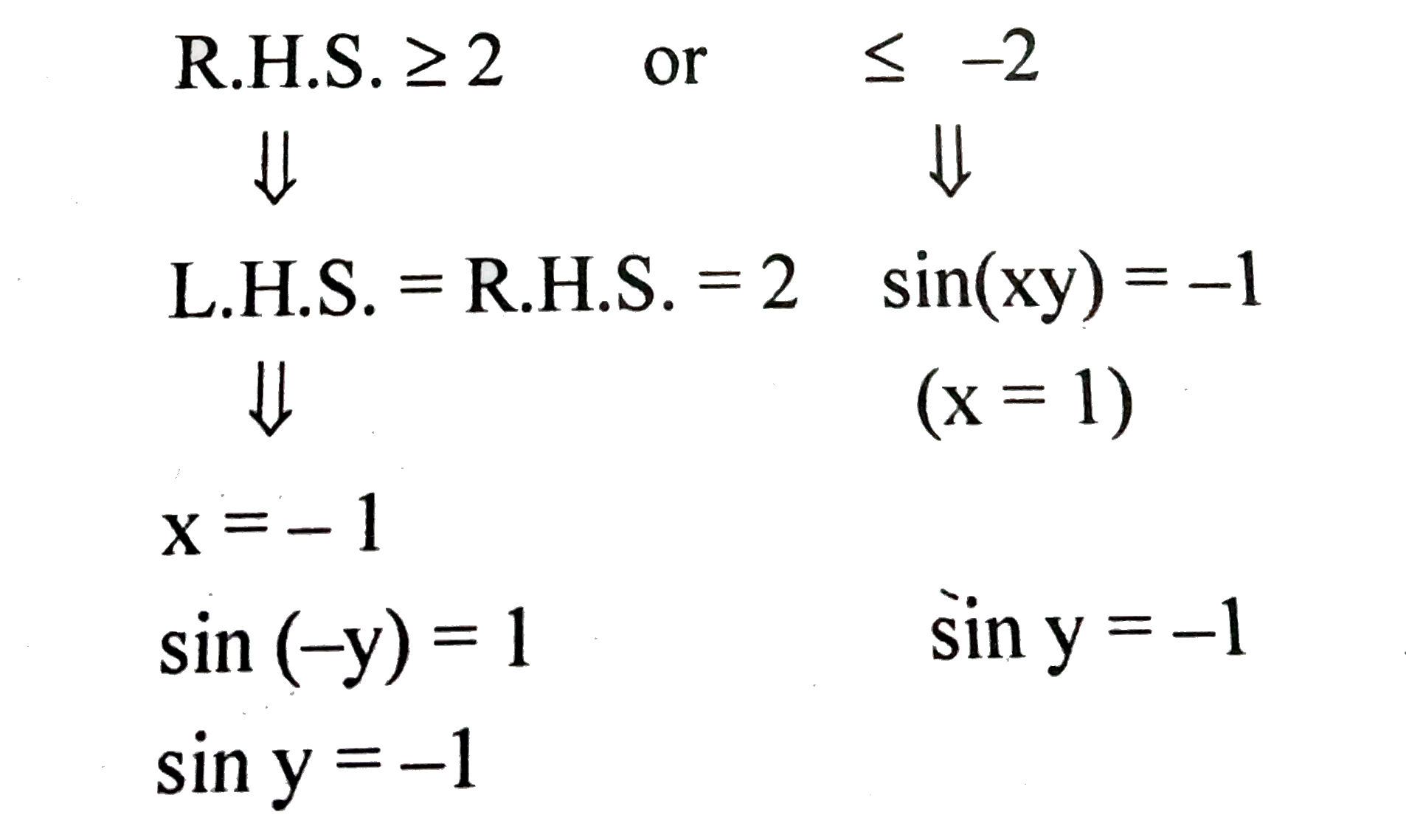
y=2nπ/π2,n∈I
Hence pair of straight lines.
|
Similar Questions
Knowledge Check
The number of ordered pair(s) (x,y) of real numbers satisfying the equation 1+x2+2xsin(cos−1y)=0, is :
A0B1C2D3If x and y satisfy te equation xy−2x2−9x+3y−16=0 then
Anumber of ordered pair (x,y) is 4 where x,y∈ZBnumber of ordered paire (x,y) is 1 where x,y∈NCif x≥y,x,y∈N then number of ordered pair is zeroDif x≤y,x,y∈N then number of ordered pairs are twoIf ax2+bx+c=0 has imaginary roots and a - b + c > 0 .
then the set of point (x, y) satisfying the equation
∣∣a(x2+ya)+(b+1)x+c∣∣=∣∣ax2+bx+c∣∣+|x+y|
of the region in the xy- plane which isAon or above the bisector of I and III quadrantBon or above the bisector of II and IV quadentCon or below the bisector of I and III quadrantDon or below the bisector of II and IV quadrant .
The number of ordered pair (x, y) satisfying the equation sin2(x+y)+cos2(x−y)=1 which lie on the circle x2+y2=π2 is _________.
View SolutionAll the pairs (x,y) that satisfy the inequality
2√sin2x−2sinx+5.14sin2y≤1 also satisfy the equation :
View SolutionIf x and y satisfy te equation xy−2x2−9x+3y−16=0 then
View SolutionThe number of ordered pairs which satisfy the equation x2+2xsin(xy)+1=0 are (where y∈[0,2π] ) 1 (b) 2 (c) 3 (d) 0
View SolutionThe number of x in (0,2π) satisfying the equation 1+sin2x=sinx+sin2x is
View Solution
