(Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be
To solve the allocation problem step by step, we will follow the linear programming method.
Step 1: Define the Variables
Let:
- X = hectares of land allocated for crop X
- Y = hectares of land allocated for crop Y
Step 2: Write the Objective Function
The profit from crops X and Y per hectare are given as Rs 10,500 and Rs 9,000 respectively. Therefore, the objective function to maximize the profit Z can be expressed as:
Z=10,500X+9,000Y
Step 3: Write the Constraints
1. The total land available is 50 hectares:
X+Y≤50
2. The herbicide requirement is given as:
- Crop X requires 20 liters per hectare
- Crop Y requires 10 liters per hectare
- The total available herbicide is 800 liters:
20X+10Y≤800
3. Non-negativity constraints:
X≥0,Y≥0
Step 4: Simplify the Constraints
1. From the herbicide constraint, we can simplify:
20X+10Y≤800⟹2X+Y≤80
(by dividing the entire inequality by 10)
Step 5: List the Constraints
Now we have the following constraints:
1. X+Y≤50
2. 2X+Y≤80
3. X≥0
4. Y≥0
Step 6: Find the Points of Intersection
To graph the constraints, we need to find the points where the lines intersect:
1. For X+Y=50:
- If X=0, then Y=50 (Point A: (0,50))
- If Y=0, then X=50 (Point B: (50,0))
2. For 2X+Y=80:
- If X=0, then Y=80 (Point C: (0,80))
- If Y=0, then X=40 (Point D: (40,0))
Step 7: Determine the Feasible Region
Now we plot the lines on a graph and identify the feasible region, which is bounded by the constraints:
- The feasible region will be below both lines and within the first quadrant (where X and Y are non-negative).
Step 8: Identify Corner Points
The corner points of the feasible region are:
1. (0,0)
2. (0,50)
3. (40,0)
4. The intersection of X+Y=50 and 2X+Y=80:
- Solve these equations:
Y=50−X(from the first equation)
Substitute into the second:
2X+(50−X)=80⟹X+50=80⟹X=30
Then, Y=50−30=20 (Point E: (30,20))
Step 9: Evaluate the Objective Function at Each Corner Point
Now we calculate the profit Z at each corner point:
1. At (0,0):
Z=10,500(0)+9,000(0)=0
2. At (0,50):
Z=10,500(0)+9,000(50)=450,000
3. At (40,0):
Z=10,500(40)+9,000(0)=420,000
4. At (30,20):
Z=10,500(30)+9,000(20)=315,000+180,000=495,000
Step 10: Determine the Maximum Profit
The maximum profit occurs at the point (30,20) with:
Maximum Profit=495,000
Final Answer
The maximum profit of Rs 495,000 occurs when 30 hectares are allocated for crop X and 20 hectares for crop Y.
---
Let:
- X = hectares of land allocated for crop X
- Y = hectares of land allocated for crop Y
The profit from crops X and Y per hectare are given as Rs 10,500 and Rs 9,000 respectively. Therefore, the objective function to maximize the profit Z can be expressed as:
Z=10,500X+9,000Y
1. The total land available is 50 hectares:
X+Y≤50
2. The herbicide requirement is given as:
- Crop X requires 20 liters per hectare
- Crop Y requires 10 liters per hectare
- The total available herbicide is 800 liters:
20X+10Y≤800
3. Non-negativity constraints:
X≥0,Y≥0
1. From the herbicide constraint, we can simplify:
20X+10Y≤800⟹2X+Y≤80
(by dividing the entire inequality by 10)
Now we have the following constraints:
1. X+Y≤50
2. 2X+Y≤80
3. X≥0
4. Y≥0
To graph the constraints, we need to find the points where the lines intersect:
1. For X+Y=50:
- If X=0, then Y=50 (Point A: (0,50))
- If Y=0, then X=50 (Point B: (50,0))
- If X=0, then Y=80 (Point C: (0,80))
- If Y=0, then X=40 (Point D: (40,0))
Now we plot the lines on a graph and identify the feasible region, which is bounded by the constraints:
- The feasible region will be below both lines and within the first quadrant (where X and Y are non-negative).
The corner points of the feasible region are:
1. (0,0)
2. (0,50)
3. (40,0)
4. The intersection of X+Y=50 and 2X+Y=80:
- Solve these equations:
Y=50−X(from the first equation)
Substitute into the second:
2X+(50−X)=80⟹X+50=80⟹X=30
Then, Y=50−30=20 (Point E: (30,20))
Now we calculate the profit Z at each corner point:
1. At (0,0):
Z=10,500(0)+9,000(0)=0
2. At (0,50):
Z=10,500(0)+9,000(50)=450,000
3. At (40,0):
Z=10,500(40)+9,000(0)=420,000
4. At (30,20):
Z=10,500(30)+9,000(20)=315,000+180,000=495,000
The maximum profit occurs at the point (30,20) with:
Maximum Profit=495,000
The maximum profit of Rs 495,000 occurs when 30 hectares are allocated for crop X and 20 hectares for crop Y.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A8videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B15videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
Similar Questions
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two of goods X and Y. To produce one unit X, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of Y. If X and Y are priced at Rs. 100 and Rs. 120 per unit respectively to should be producer use his resources to maximize the total revenue?
View Solution(a) In general, which metals are expected to occur in the native state in nature ?
(b) A certain metal M occurs in three compounds namely X,Y and Z.X has 15% of M,Y has 66% of M and Z has 71% of M. If we extract M from X,Y and Z, it costs Rs.35perkg,Rs.45perkg and Rs.100perkg respectively. Out of X,Y and Z which material can be considered as an ore of M ?View Solution
Knowledge Check
- Question 1 - Select One
Greek yogurt—a strained form of cultured yogurt—has grown enormously in popularity in the United States since it was first introduced in the country in the late 1980s.
From 2011 to 2012 alone, sales of Greek yogurt in the US increased by 50 percent. The resulting increase in Greek yogurt production has forced those involved in the business to address the detrimental effects that the yogurt-making process may be having on the environment. Fortunately, farmers and others in the Greek yogurt business have found many methods of controlling and eliminating most environmental threats. Given these solutions as well as the many health benefits of the food, the advantages of Greek yogurt 1 outdo––––––– the potential drawbacks of its production.
[1] The main environmental problem caused by the production of Greek yogurt is the reation of acid whey as a by-product. [2] Because it requires up to four times more milk to make than conventional yogurt does, Greek yogurt produces larger amounts of acid whey, which is difficult to dispose of. [3] To address the problem of disposal, farmers have found a number of uses for acid whey. [4] They can add it to livestock feed as a protein (2) supplement, and people can make their own Greek-style yogurt at home by straining regular yogurt–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––. [5] If it is improperly introduced into the environment, acid-whey runoff (3) can pollute waterways––––––––––––––––––––––––, depleting the oxygen content of streams and rivers as it decomposes. [6] Yogurt manufacturers, food (4)scientists, and––––––––––––––––government officials are also working together to develop additional solutions for reusing whey.(5).
(6) Though these conservation methods can be costly and time-consuming, they are well worth the effort–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––.Nutritionists consider Greek yogurt to be a healthy food: it is an excellent source of calcium and protein, serves (7) to be––––––– a digestive aid, and 8 'ul("it contains")fewcalories∈itsunsweete≠dlow−andnon−fatforms.Greekyogurtisslightlylower∈sugarandcarbohydratesthanconventionalyogurtis.(9)ul("Also"),∵itismoreconcentrated,Greekyogurtconta∈sslightlymoreprote∈perserv∈g,therebyhelπngpeop≤stay(10)ul("satiated")forlon≥rperiodsoftime.Thesehea<hbe≠fitshavepromptedGreekyogurt’srecentsur≥∈popa––rity.Infact,Greekyogurtcanbefound∈an∈creasingνmberof∏uctssuchassnackf∞dandozendesserts.Becausecon∑ersreaptheνtritionalbe≠fitsofGreekyogurtand⊃portthosewhomakeandsell(11)ul("it, therefore farmers") and businesses should continue finding safe and effective methods of producing the food.ANO CHANGEBdefeatCoutperformDoutweigh
Two liquids X and Y boil at 110∘C and 130∘C, respectively. Which one of them has higher vapour pressure at 50∘C?
View SolutionA farm is engaged in breeding pigs. The pigs are fed on various products grown on the farm. In view of the need to ensure certain nutrient constituents (call them X,Y and Z), it is necessary to buy two additional products, say, A and B. One unit of product A contains 36 units of X, 3 units of Y, and 20 units of Z. One unit of product B contains 6 units of X, 12 units of Y and 10 units of Z. The minimum requirement of X, Y and Z is 108 units respectively. Product A costs LRs. 20 per unit and product B costs Rs. 40 per unit. Formulate the above as a linear programming problem to minimize the total cost, and solve the problem by using graphical method.
View SolutionA manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below:
Market Products
I 10.000 2.000 18.000
II 6.000 20.000 8.000
(a) If unit sale prices of x, y and z are Rs 2.50, Rs 1.50 and Rs 1.00, respectively, find the total revenue in each market with the help of matrix algebra.(b) If the unit costs of the above three commodities are Rs 2.00, Rs 1.00 and 50paise respectively. Find the gross profit.View SolutionA company sells two different products A and B. The two products are produced in a common production process and are sold in two different markets. The production process has a total capacity of 45000 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 7000 ad that of B is 10,000. If the profit is Rs. 60 per unit for the product A and Rs. 40 per unit for the product B, how many units of each product should be sold to maximize profit? Formulate the problem as LPP.
View SolutionX and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.
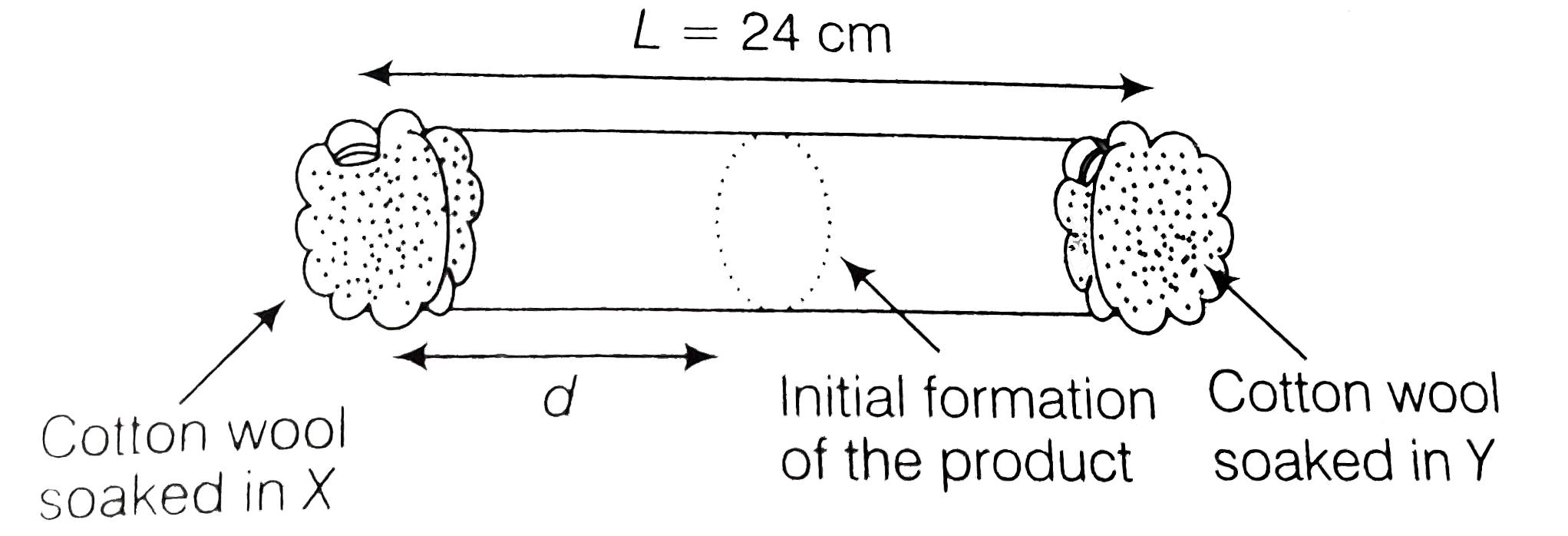
The value of d in cm (shown in figure), as estimated from Graham's law, isView SolutionX and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.

The value of d in cm (shown in figure), as estimated from Graham's law, isView SolutionCenters of two similar coils P and Q having same number of turns are located at the coordinates (0.4,0) and (0,0.3) such that the plane of coils are perpendicular to X-and Y-axis respectively. The areas of cross section of coils P and Q are in the ration 4:3 Coil P has 16 A current in clockwise direction and coil Q has 9√3A current in anticlockwise direction as seen from the origin. A small compass needle is placed at the origin. Find the deflection in the needle, assuming the earth's magnetic field negligible and the radii of the coils very small compared to their distances from the origin.
View Solution

