Aman walked 63m due east. He then turned and walkeed for 16 m due north. How far is he from the starting point ?
The correct Answer is:65 m
To find out how far Aman is from his starting point after walking 63 meters east and then 16 meters north, we can use the Pythagorean theorem. Here’s a step-by-step solution:
Step 1: Understand the Movement
Aman starts at point A and walks 63 meters east to point B. Then, he turns and walks 16 meters north to point C. We need to find the distance from point A to point C.
Step 2: Draw the Diagram
Draw a right triangle where:
- Point A is the starting point.
- Point B is 63 meters east of A.
- Point C is 16 meters north of B.
This forms a right triangle with:
- AB = 63 meters (horizontal leg)
- BC = 16 meters (vertical leg)
Step 3: Apply the Pythagorean Theorem
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Where:
- AC is the hypotenuse (the distance from A to C),
- AB is one leg (63 meters),
- BC is the other leg (16 meters).
Step 4: Substitute the Values
Substituting the values into the equation:
AC2=632+162
Step 5: Calculate the Squares
Now calculate 632 and 162:
- 632=3969
- 162=256
Step 6: Add the Squares
Now add these two results:
AC2=3969+256=4225
Step 7: Take the Square Root
To find AC, take the square root of 4225:
AC=√4225=65
Final Answer
Aman is 65 meters away from the starting point.
---
Aman starts at point A and walks 63 meters east to point B. Then, he turns and walks 16 meters north to point C. We need to find the distance from point A to point C.
Draw a right triangle where:
- Point A is the starting point.
- Point B is 63 meters east of A.
- Point C is 16 meters north of B.
This forms a right triangle with:
- AB = 63 meters (horizontal leg)
- BC = 16 meters (vertical leg)
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Where:
- AC is the hypotenuse (the distance from A to C),
- AB is one leg (63 meters),
- BC is the other leg (16 meters).
Substituting the values into the equation:
AC2=632+162
Now calculate 632 and 162:
- 632=3969
- 162=256
Now add these two results:
AC2=3969+256=4225
To find AC, take the square root of 4225:
AC=√4225=65
Aman is 65 meters away from the starting point.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - CHALLENGE1videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - REVISIONS EXERCISE15videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 12.211videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - SYMMETRYEXERCISE - Exercise 19B13videos
SYMMETRY
- BOOK - ICSECHAPTER - UNITARY METHODEXERCISE - EXERCISE16videos
UNITARY METHOD
Similar Questions
A man goes 15 m due west and then 8 m due north. How far is he from the starting point?
View SolutionA man goes 24m due wes and then 10 m due north. How far is he from the staring point?
View SolutionA man goes 150 m due east and then 200 m due north. How far is he from the starting point ?
View SolutionA man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
View SolutionA man travels 90 km due East and then 56 km due South. How far is the form the starting point ?
View SolutionA man goes 24m due west and then 7m due north. How far is he from the starting point? (a) 31m (b) 17m (c) 25m (d) 26m
View SolutionA man goes 10m due east and then 24 m due north. Find the distance from the starting point.
View SolutionA man goes 10 m due east and than 24 m due north. Find the distance from the starting point.
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
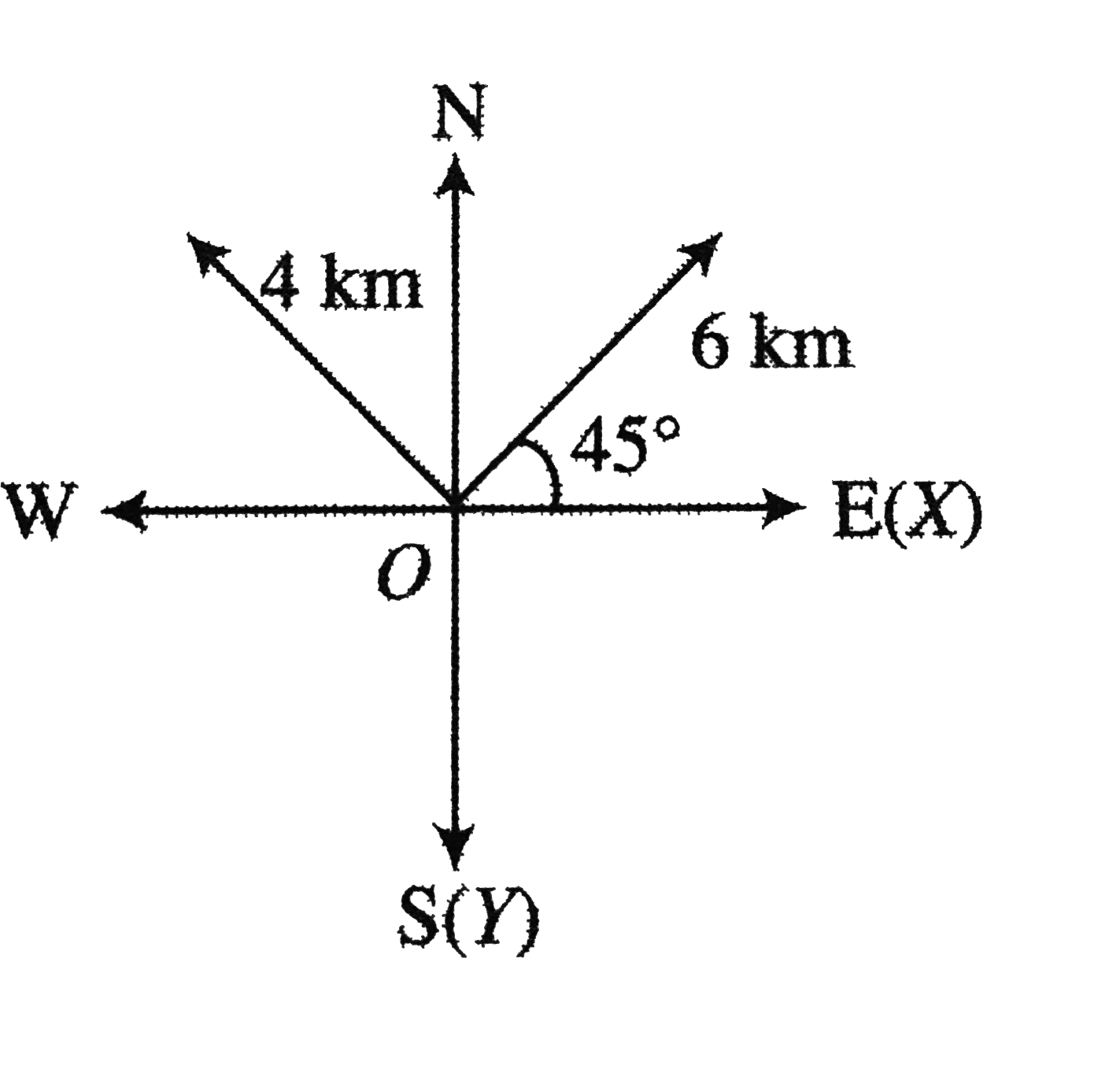 View Solution
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
 View Solution
View Solution
