Amit was playing a number card game. In the game, some number cards (having both +ve or -ve numbers) are arranged in a row such that they are following an arithmetic progression. On his first turn, Amit picks up 6th and 14th card and finds their sum to be -76. On the second turn he picks up 8th and 16th card and finds their sum to be −96.
Based on the above information, answer the following questions.
What is the sum of 9thand15th card ?

Step by step video & image solution for Amit was playing a number card game. In the game, some number cards (having both +ve or -ve numbers) are arranged in a row such that they are following an arithmetic progression. On his first turn, Amit picks up 6th and 14th card and finds their sum to be -76. On the second turn he picks up 8th and 16th card and finds their sum to be - 96. Based on the above information, answer the following questions. What is the sum of 9^(th) and 15^(th) card ? <BR> by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The sum of the 6th and 15th elements of an arithmetic progression is equal to the sum of 7th 10th and 12th elements of the same progression. Which elements of the series should necessarily be equal to zero
A10thB8thC1stD9thOut of 6 numbers, the sum of the first 5 numbers is 7 times the 6th number. If their average is 136, then the 6th number is:
6 संख्याओं में से, पहली 5 संख्याओं का जोड़ छठी संख्या से 7 गुना है | यदि उनका औसत 136 है, तो छठी संख्या कौन सी है ?A96B102C84D116Out of 6 numbers, the sum of the first 5 numbers is 7 times the 6th number. If their average is 136, then the 6th number is:
A116B102C84D96
If sum of the 3rd and the 8th terms of an AP is 7 and the sum of the 7th and 14th terms is -3, then find the 10th term.
View SolutionThe sum of the 6th and 9 th terms ofan AP is 101 and the sum of the 10th and 16th terms is 178. Find the first three terms of the AP.
View SolutionThe sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
View SolutionPlaying cards
(a) From a pack of cards the following cards are kept face down:
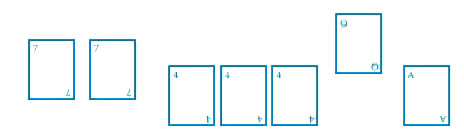 Suhail wins if he picks up a face card. Find the probability of Suhail winning?
Suhail wins if he picks up a face card. Find the probability of Suhail winning?
View SolutionThe sum of the 4th and the 8 the terms of an AP is 24 and the sum of its 6th and 10th terms is 44. Find its first term.
View Solution
