An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 400 is made on each first class ticket and a profit of Rs. 300 is made on each second class ticket. The airline reserves at least 20 seats for first class. However, at least four times as many passengers prefer to travel by second class then by first class. Determine how many tickets of each type must be sold to maximise profit for the airline. Form an LPP and solve it graphically.
The correct Answer is:40 passengers from first clas and 160 passengers from second class, Maximum profit =Rs.1,12,000
To solve the problem, we need to formulate a Linear Programming Problem (LPP), define the constraints, and then solve it graphically. Here’s a step-by-step solution:
Step 1: Define the Variables
Let:
- x = number of first class tickets sold
- y = number of second class tickets sold
Step 2: Formulate the Objective Function
The profit from selling first class tickets is Rs. 400 per ticket, and from second class tickets, it is Rs. 300 per ticket. Therefore, the objective function to maximize profit Z is:
Z=400x+300y
Step 3: Define the Constraints
1. The total number of passengers cannot exceed 200:
x+y≤200
2. At least 20 seats must be reserved for first class:
x≥20
3. At least four times as many passengers prefer to travel by second class than by first class:
y≥4x
4. Non-negativity constraints:
x≥0,y≥0
Step 4: Graph the Constraints
To graph the constraints, we will convert each inequality into an equation:
1. x+y=200
2. x=20
3. y=4x
Next, we plot these equations on a graph:
- The line x+y=200 intersects the axes at (200, 0) and (0, 200).
- The line x=20 is a vertical line at x=20.
- The line y=4x passes through the origin and has a slope of 4.
Step 5: Identify the Feasible Region
The feasible region is determined by the area that satisfies all constraints. It will be bounded by the lines we plotted, and we will find the corner points of this region.
Step 6: Find the Corner Points
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+y=200 and x=20:
20+y=200⟹y=180(Point A: (20, 180))
2. Intersection of x+y=200 and y=4x:
x+4x=200⟹5x=200⟹x=40⟹y=160(Point B: (40, 160))
3. Intersection of y=4x and x=20:
y=4(20)=80(Point C: (20, 80))
Step 7: Evaluate the Objective Function at Each Corner Point
Now we evaluate Z=400x+300y at each corner point:
1. At Point A (20, 180):
Z=400(20)+300(180)=8000+54000=62000
2. At Point B (40, 160):
Z=400(40)+300(160)=16000+48000=64000
3. At Point C (20, 80):
Z=400(20)+300(80)=8000+24000=32000
Step 8: Determine the Maximum Profit
The maximum profit occurs at Point B (40, 160) with a profit of Rs. 64000.
Conclusion
To maximize profit, the airline must sell:
- 40 first class tickets
- 160 second class tickets
Let:
- x = number of first class tickets sold
- y = number of second class tickets sold
The profit from selling first class tickets is Rs. 400 per ticket, and from second class tickets, it is Rs. 300 per ticket. Therefore, the objective function to maximize profit Z is:
Z=400x+300y
1. The total number of passengers cannot exceed 200:
x+y≤200
2. At least 20 seats must be reserved for first class:
x≥20
3. At least four times as many passengers prefer to travel by second class than by first class:
y≥4x
4. Non-negativity constraints:
x≥0,y≥0
To graph the constraints, we will convert each inequality into an equation:
2. x=20
3. y=4x
- The line x=20 is a vertical line at x=20.
- The line y=4x passes through the origin and has a slope of 4.
The feasible region is determined by the area that satisfies all constraints. It will be bounded by the lines we plotted, and we will find the corner points of this region.
The corner points of the feasible region can be found by solving the equations of the lines:
1. Intersection of x+y=200 and x=20:
20+y=200⟹y=180(Point A: (20, 180))
2. Intersection of x+y=200 and y=4x:
x+4x=200⟹5x=200⟹x=40⟹y=160(Point B: (40, 160))
3. Intersection of y=4x and x=20:
y=4(20)=80(Point C: (20, 80))
Now we evaluate Z=400x+300y at each corner point:
1. At Point A (20, 180):
Z=400(20)+300(180)=8000+54000=62000
2. At Point B (40, 160):
Z=400(40)+300(160)=16000+48000=64000
3. At Point C (20, 80):
Z=400(20)+300(80)=8000+24000=32000
The maximum profit occurs at Point B (40, 160) with a profit of Rs. 64000.
To maximize profit, the airline must sell:
- 40 first class tickets
- 160 second class tickets
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.1
10 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.2
11 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A
8 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
View SolutionAn aeroplane can carry a maximum of two passengers. A profit of Rs. 1000 is made on each executive clas ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However at least 4 times as many passengers prefer to travel by economy clas than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
View Solution
Knowledge Check
The main reserve food material of class Chlorophyceae is :
AfatBstarchCglycogenDvolutinBoys and girls in a class are writing letters. There are twice as many girls as boys in the class, and each girl writes 3 more letters than each boy. If boys write 24 of the 90 total letters written by the class, how many letters does each boy write?
A3B4C5D8Refer to the figures, (A, B and C) and arrange them in an order of list class lever, second class lever and third class lever.
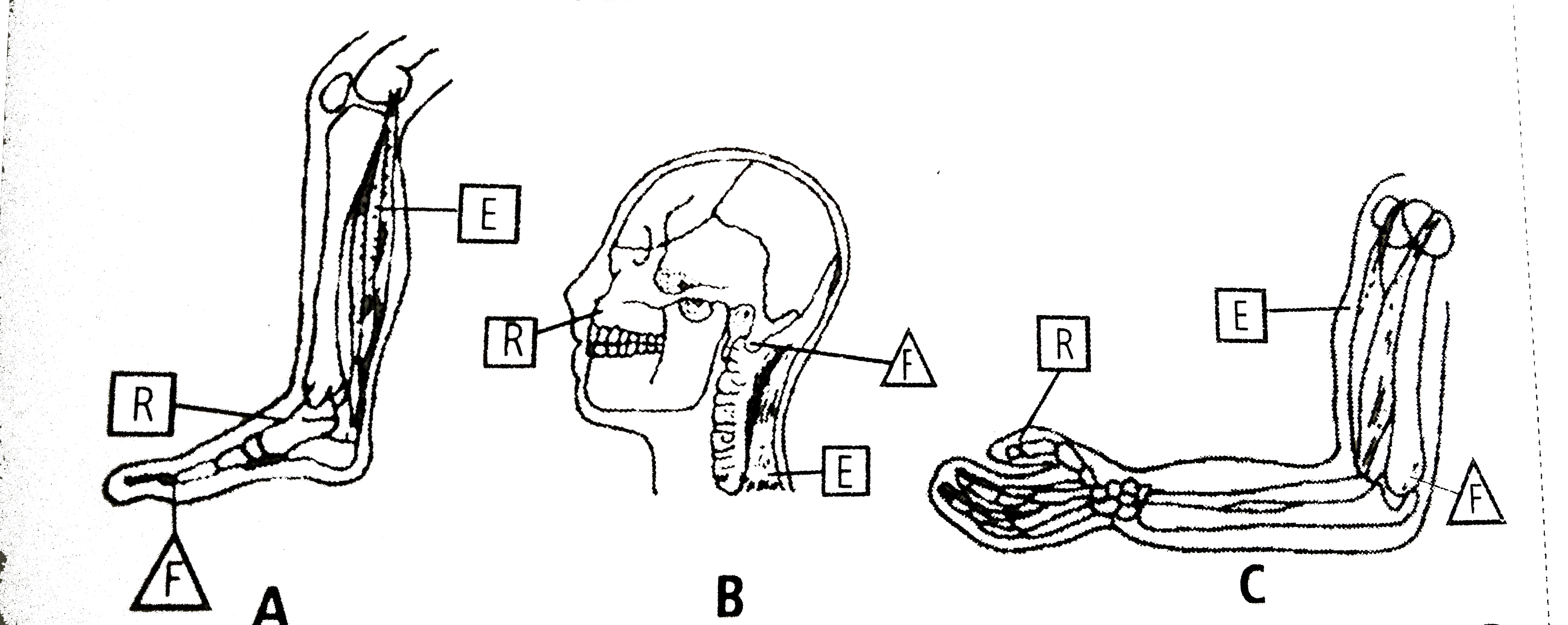 AB,A,CBC,A,BCC,B,ADA,C,B
AB,A,CBC,A,BCC,B,ADA,C,B
Class- 7 Math profit and loss
View SolutionFirst class lever and Second class lever
View SolutionIn a class A of 25 students, 20 passed in first class; in another class B of 30 students, 24 passed in first class. In which class was a greater fraction of students getting first class?
View SolutionIn a class A of 25 students, 20 passed in first class; in another class B of 30 students, 24 passed in first class. In which class was a greater fraction of students getting first class?
View SolutionIn how many classes angiosperms are divided?
View Solution
