An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results: Firm A Firm B No. of wage earners 586 648 Mean of monthly wages Rs 5253 Rs 5253 Variance of the distribution of wages 100 121 (i) Which firm A or B pays larger amount as monthly wages? (ii) Which firm, A or B, shows greater variability in individual wages?
To solve the given problem, we will break it down into two parts as specified in the question.
Given Data:
- Firm A:
- Number of wage earners (n_A) = 586
- Mean of monthly wages (μ_A) = Rs 5253
- Variance (σ²_A) = 100
- Firm B:
- Number of wage earners (n_B) = 648
- Mean of monthly wages (μ_B) = Rs 5253
- Variance (σ²_B) = 121
Part (i): Which firm A or B pays a larger amount as monthly wages?
To find out which firm pays a larger total amount in monthly wages, we will calculate the total wages paid by each firm using the formula:
Total Wages=Number of Wage Earners×Mean Monthly Wage
1. Calculate Total Wages for Firm A:
Total WagesA=nA×μA=586×5253
Total WagesA=307,8258 Rs
2. Calculate Total Wages for Firm B:
Total WagesB=nB×μB=648×5253
Total WagesB=3,403,944 Rs
3. Compare Total Wages:
- Total Wages for Firm A = Rs 3,078,258
- Total Wages for Firm B = Rs 3,403,944
Since Rs 3,403,944 (Firm B) > Rs 3,078,258 (Firm A), Firm B pays a larger amount as monthly wages.
Part (ii): Which firm, A or B, shows greater variability in individual wages?
To determine which firm shows greater variability in individual wages, we need to calculate the standard deviation for each firm. The standard deviation (σ) is the square root of the variance (σ²).
1. Calculate Standard Deviation for Firm A:
\sigma_A = \sqrt{σ²_A} = \sqrt{100} = 10
2. Calculate Standard Deviation for Firm B:
σB=√σ²B=√121=11
3. Compare Standard Deviations:
- Standard Deviation for Firm A = 10
- Standard Deviation for Firm B = 11
Since 11 (Firm B) > 10 (Firm A), Firm B shows greater variability in individual wages.
Final Answers:
(i) Firm B pays a larger amount as monthly wages.
(ii) Firm B shows greater variability in individual wages.
- Firm A:
- Number of wage earners (n_A) = 586
- Mean of monthly wages (μ_A) = Rs 5253
- Variance (σ²_A) = 100
- Number of wage earners (n_B) = 648
- Mean of monthly wages (μ_B) = Rs 5253
- Variance (σ²_B) = 121
Total WagesA=nA×μA=586×5253
Total WagesA=307,8258 Rs
Total WagesB=nB×μB=648×5253
Total WagesB=3,403,944 Rs
- Total Wages for Firm A = Rs 3,078,258
- Total Wages for Firm B = Rs 3,403,944
\sigma_A = \sqrt{σ²_A} = \sqrt{100} = 10
σB=√σ²B=√121=11
- Standard Deviation for Firm A = 10
- Standard Deviation for Firm B = 11
(i) Firm B pays a larger amount as monthly wages.
(ii) Firm B shows greater variability in individual wages.
Topper's Solved these Questions
Similar Questions
An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results: Firm A Firm B No. of wages earners 586 684 Mean of monthly wages Rs. 5253 Rs. 5253 Variance of the distribution of wages 100 121 Which firm A or B pays to larger mount as monthly wages? Which firm A or B shows greater variability in individual wages?
View SolutionAn analysis of the weekly wages paid to workers in two firms A and B, belonging to the same industry gives the following results; Firm A Firm B No. of wages earners 586 648 Average weekly wages Rs. 2. Rs. 47.5 Distribution of wages 100 121 Which firm A or B pays out larger amount as weekly wages? Which firm A or B has greater variability in individual wages?
View SolutionAn analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following result and no. of workers of firm A and B are 586 and 648 respectively No. of wage earners Firm A Firm B Mean of monthly wages Rs 5253 Rs 5253 Variance of the distribution 100 121 of wages (i) Which firm A or B pays larger amount as monthly wages? (ii) Which firm, A or B, show greater variability in individual wages?
View SolutionAn analysis of monthly wages paid to the works of two firms A and B belonging to the same industry gives the following results: Firm A Firm B Number of workers 1000 1200 Average monthly wages Rs. 2800 Rs. 2800 Variance of distribution of wages 100 169 In which firm, A or B is there greater variability in individual wages?
View SolutionAn analysis of monthly wages paid to workers intwo firms A and B, belonging to the same industry, gives the following results:

(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm A or B shows greater variability in individual wages?View SolutionFor two firms A and B belonging to the same industry the following data is given
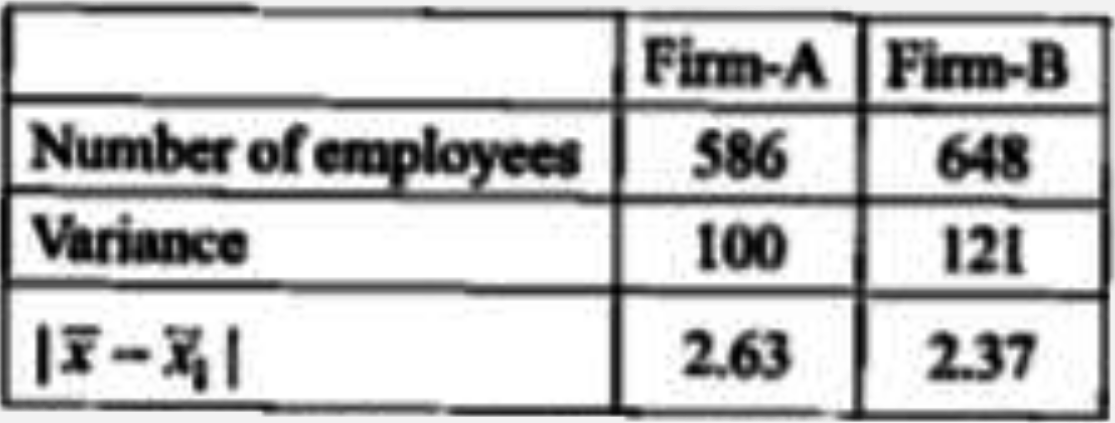
Find the combined variance of the two firmsView SolutionAn analysis of daily wages of casual laboures in two firms A and B belonging to the same industry gives the following result :

If the combined mean is Rs 116.82 find the standard deviation of wages of all casual labourers in the two firms taken in together .View SolutionIn two factories A and B engaged in the same industrial area, the average weekly wages (in rupees) and the standard deviations are as follows:

(i) Which factory, A or B, pays out a larger amount as weekly wages?
(ii) Which factory, A or B, has greater variability in individual wages?View SolutionTwo plants A and B of a factory show following results about the number of workers and the wages paid to them. Plant A Plant B No. of workers 5000 6000 Average monthly wages Rs. 2500 Rs. 2500 Variance of distribution of wages 81 100 In which plant A or B is there greater variability in individual wages?
View SolutionTwo plants A and B of a factory show following results about the number of workers and the wages paid to them. A B
No. of workers 5000 6000
Average monthly wages Rs 2500 Rs 2500
Variance of distribution 81 100
of wages.In which plant, A or B is there greater variability in individual wages?View Solution

