An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round ? Remember, circumference of a circle can be obtained by using the expression c=2πr, where r is the radius of the circle.
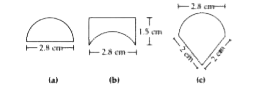
The correct Answer is:figure (b)
Step by step video, text & image solution for An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round ? Remember, circumference of a circle can be obtained by using the expression c = 2pi r, where r is the radius of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.2)11videos
MENSURATION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - NCERT Section (Exercise 11.3)10videos
MENSURATION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Solved Examples21videos
MENSURATION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - Olympiad/HOTS Corner15videos
LINEAR EQUATIONS IN ONE VARIABLE
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PLAYING WITH NUMBERSEXERCISE - Olympiad/HOTS Corner6videos
PLAYING WITH NUMBERS
Similar Questions
A particle is moving in a circle of radius R with constant speed. The time period of particle is T=1s. In a time t=T6, the difference between the average speed and the average velocity of the particle is 2ms. Find the radius R (in metres) of the circle. (Take π=227)
View SolutionA particle is moving in a circle of radious R with constant speed. The time period of the particle is T = 1s. In a time interval T6, if the difference between average speed and the magnitude of average velocity of the particle is 2m/s, then report 49R50, where R is the radius of the circle (in metres) (take π=3.14 )
View Solution
Knowledge Check
- Question 1 - Select One
If the radius ( r ) of a circle is increased by 'x' units , what is the number of units by which the circumference of the circle is increased?
A. π
B. 2π
C. 2πr
D. 2πxADBCCBDA - Question 2 - Select One
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.

An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic fluxAcan chane sinusoidallyBshould either increase or decrease all the timeCmust becomes zero when induced field is maximumDnone of these - Question 3 - Select One
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
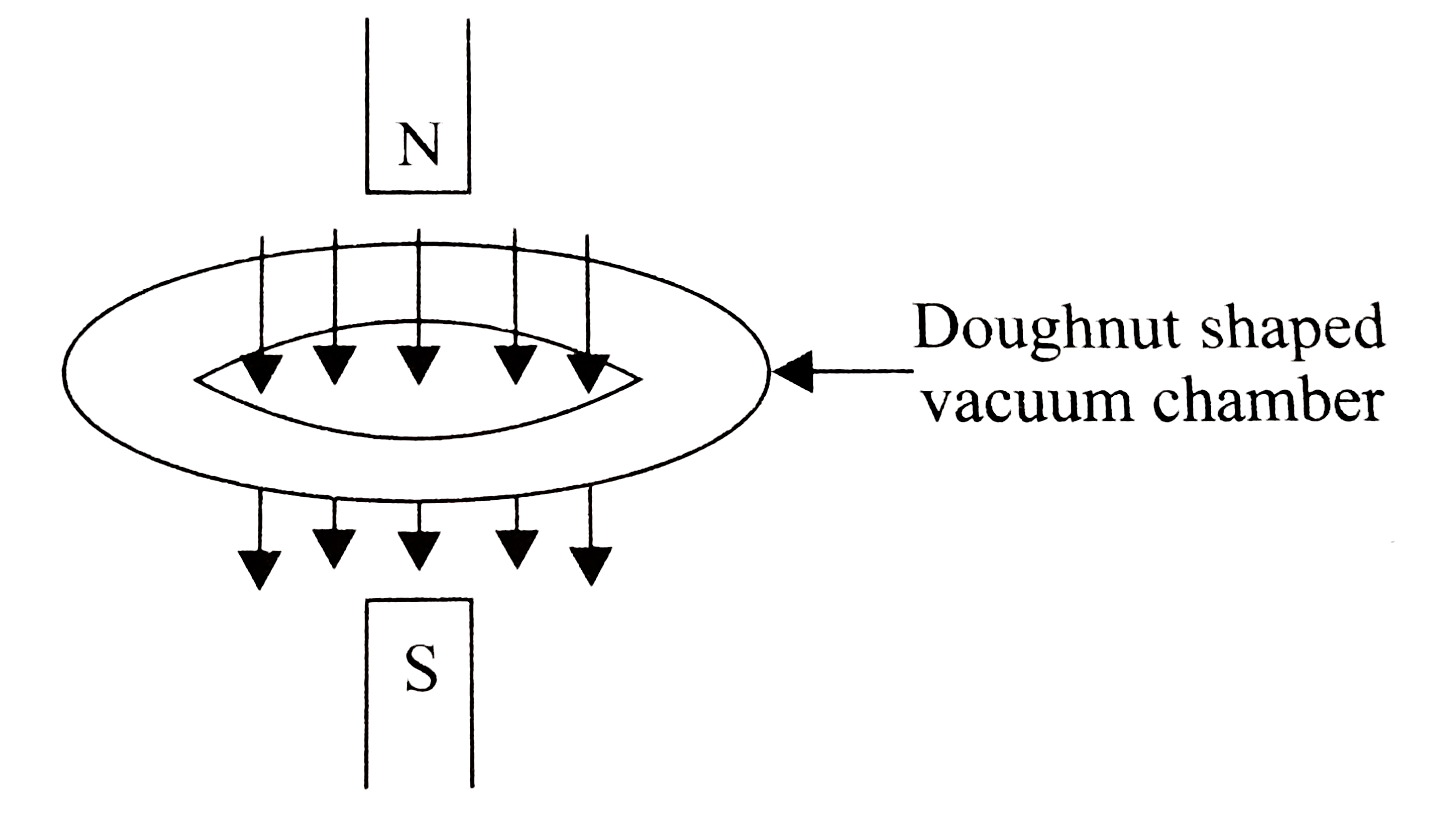
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path mustAremain constant every whereBincreases gradually which is proportional to kinetic energy of the particleCincrease gradually which is proportional to speed of the particleDnone of these
A thread having linear charge density λ is in the shape of a circular arc of radius R subtending an angle θ at the centre.
(a). Find the electric field at the centre.
(b). Using the epression obtained in part (a) find the field at the centre if the thread were emicircular
(c). Find the field at centre using the expression obtained in part (a) for the case θ→0. Is the result justified?
(d). A thread having total charge Q (uniformly distributed is in the shape of a circular arc of radius R subtending an angle θ at centre. write the expression for the field at the center. Obtain the field whenθ→0. Make sure you understand the difference in case. (c) and (d).
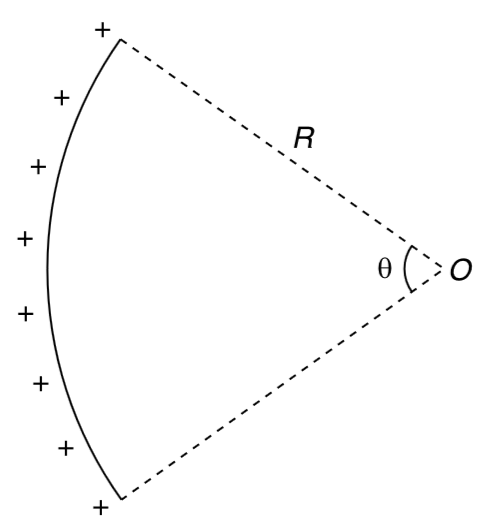 View Solution
View SolutionLinked Comprehension Type Based upon each paragraph, three multiple choice questions have to be answered. Each question has four choices: a, b, c, and d, out of which only one is correct For Problems 1-3 center is at Each side of a square has length 4 units and its (3, 4). If one of the diagonals is parallel to the line y x, then answer the following questions 1. Which of the following is not the vertex of the square? a. (1, 6) b. (5, 2) c. (1, 2) d. (4, 6) 2. The radius of the circle inscribed in the triangle formed by any three vertices is a. 2020V2 1) 2012 1) d. none of these 3. The circle inscribed in the triangle forme radius of the by any two vertices of the square and the center is b. 202 1) a. 2012 1) d. none of these v2012 1) For Problems 4-6 Tangents PA and PB are drawn to the circle (x 4) 4 from the point P on the curve y sin x, where A and B on the circle. Consider the function y f(r) represented by locus of the center of the circumcircle of triangle PAB. T answer the following questions
View Solution(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure (a) through (f)) to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is I0=12MR2 where M= mass of the fan.

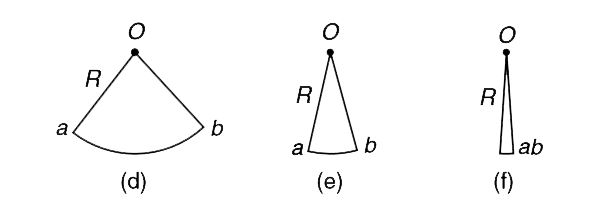
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. (f)), write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is ML23View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
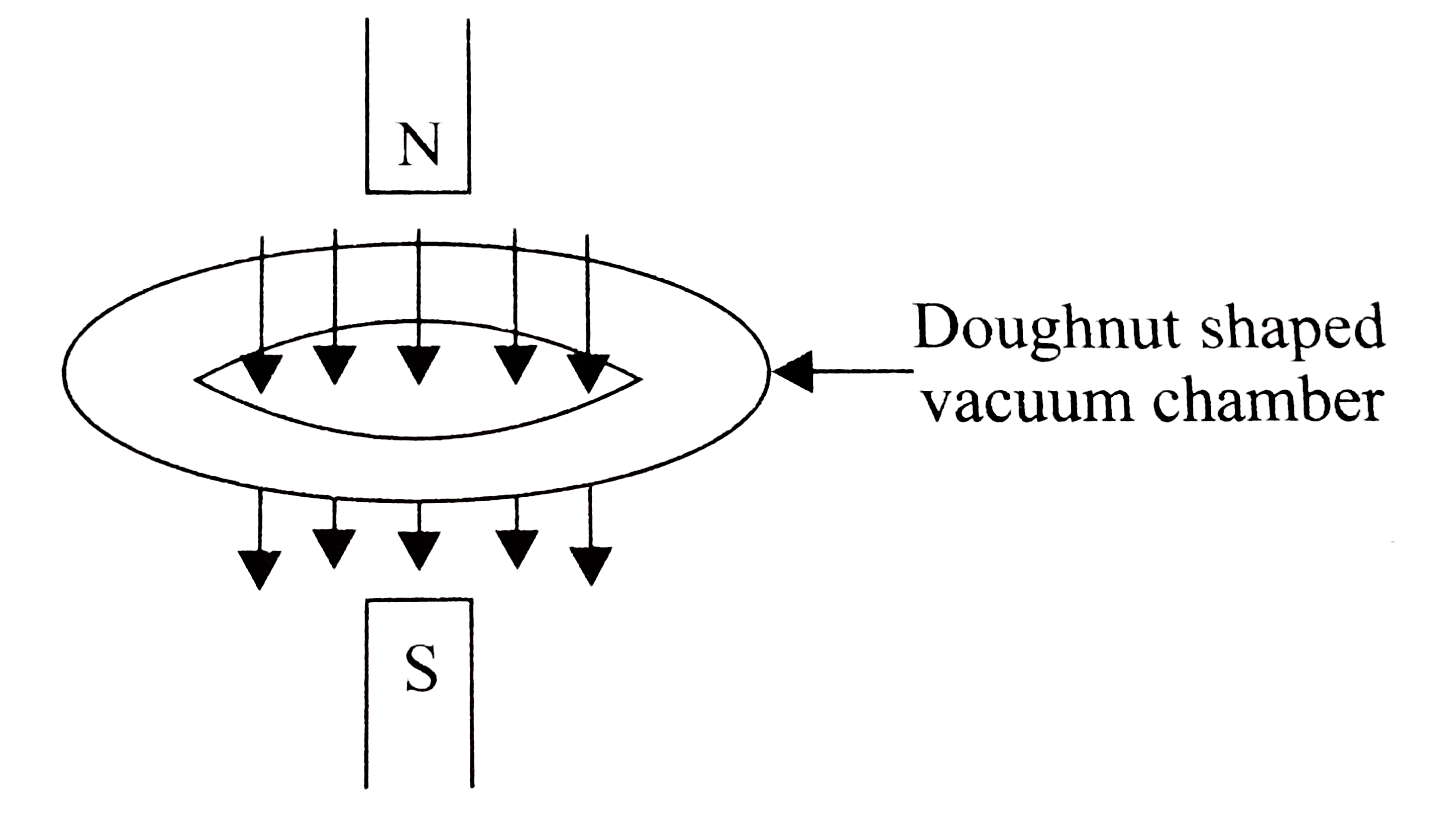
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?View SolutionThis section contains a paragraph. Based upon this paragraph, three multiple- choice question (21-23) have to be answered. Each question has four choices (a,b,c and d), out of which only one is correct.
The result obtained in electrostatics using Gauss's law can in same cases be used to obtain result in gravitational, and vice versa. This is because both follow the inverse- square law of distance. We use of the following three rules
(1) For charge in electrostatics, the corresponding quantity in gravitation is mass.
(2) Electric intensity of electrostatics corresponds to gravitational intensity, or acceleration due to gravity, in gravitation.
(3)The constant k=(4πε0)−1 of electrostatics corresponds to -G in gravitation.
The acceleration dut to gravity at the surface of the earth is g, and at a distance r from the centre of the earth is gr/R, where R is the radius of the earth. Inside a uniformly charged sphere of radius R and charge Q, the electric intensity at a distance r (r<R) from the centre has the magnitudeView Solution

