An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.
1.5h
1hr5min
2hr
1hr
The correct Answer is:D
To solve the problem step-by-step, we will follow the given information and apply the necessary calculations.
Step 1: Understand the Initial and Final Positions
- The elevator starts at a height of 10 m above the ground level.
- The final position of the elevator is –350 m, which means it is 350 m below the ground level.
Step 2: Calculate the Total Distance to be Descended
- To find the total distance the elevator needs to descend, we need to calculate the distance from the starting point (10 m) to the final point (–350 m).
- The total distance can be calculated as:
Total Distance=Final Position−Initial Position=(−350)−10
Total Distance=−350−10=−360 m
Step 3: Determine the Rate of Descent
- The elevator descends at a rate of 6 m/min.
Step 4: Use the Speed Formula to Find Time
- The formula for speed is:
Speed=DistanceTime
- Rearranging the formula to find time gives us:
Time=DistanceSpeed
- Substituting the values we have:
Time=−360 m−6 m/min
Time=3606=60 minutes
Step 5: Conclusion
- Therefore, the time it will take for the elevator to reach –350 m is 60 minutes, which is equivalent to 1 hour.
---
- The elevator starts at a height of 10 m above the ground level.
- The final position of the elevator is –350 m, which means it is 350 m below the ground level.
- To find the total distance the elevator needs to descend, we need to calculate the distance from the starting point (10 m) to the final point (–350 m).
- The total distance can be calculated as:
Total Distance=Final Position−Initial Position=(−350)−10
Total Distance=−350−10=−360 m
- The elevator descends at a rate of 6 m/min.
- The formula for speed is:
Speed=DistanceTime
- Rearranging the formula to find time gives us:
Time=DistanceSpeed
- Substituting the values we have:
Time=−360 m−6 m/min
Time=3606=60 minutes
- Therefore, the time it will take for the elevator to reach –350 m is 60 minutes, which is equivalent to 1 hour.
Topper's Solved these Questions
Similar Questions
A rock is dropped from an 80- meter cliff. How long does it take to reach the ground ?
View SolutionA long pole is made to stand against a wall in such a wat that its foot is 16 m from the wall and its top reaches a window 12 m above the ground. Find the length of the pole.
View SolutionA ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
View SolutionA lift accelerates downwards from rest at rate of 2m/s2, starting 100m above the ground. After 3 sec, an object falls out of the lift. Which will reach the ground first? What is the time interval between their striking the ground?
View SolutionA balloon is ascending at the constant rate of 9.8m/sec at a height of 98m above the ground a packet is dropped from it. If time taken by the packet to reach the ground is (1+√3λ)sec. Find λ.
(Use g=9.8m/s2)
View SolutionA ball is projected vertically up with an initial speed of 20m/s on a planet where acceleration due to gravity is 10m/s2
(a) How long does it takes to reach the highest point?
(b) How high does it rise above the point of projection?
(c) How long wil it take for the ball to reach a point 10m above the point of projection?
View SolutionA ball is thrown vertically upwards from the ground and a student gazing out of the window sees it moving upward past him at 10ms−1. The window is at 15 m above the ground level. The velocity of ball 3 s after it was projected from the ground is [Take g=10ms−2]
View SolutionA parachutist drops freely from helicopter for 20 s before the parachute opends out. Then he descends with retardation of 40ms2. The height of the helicopter from the ground level is 2500m. When he drops out, his velocity on reaching the ground will be
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
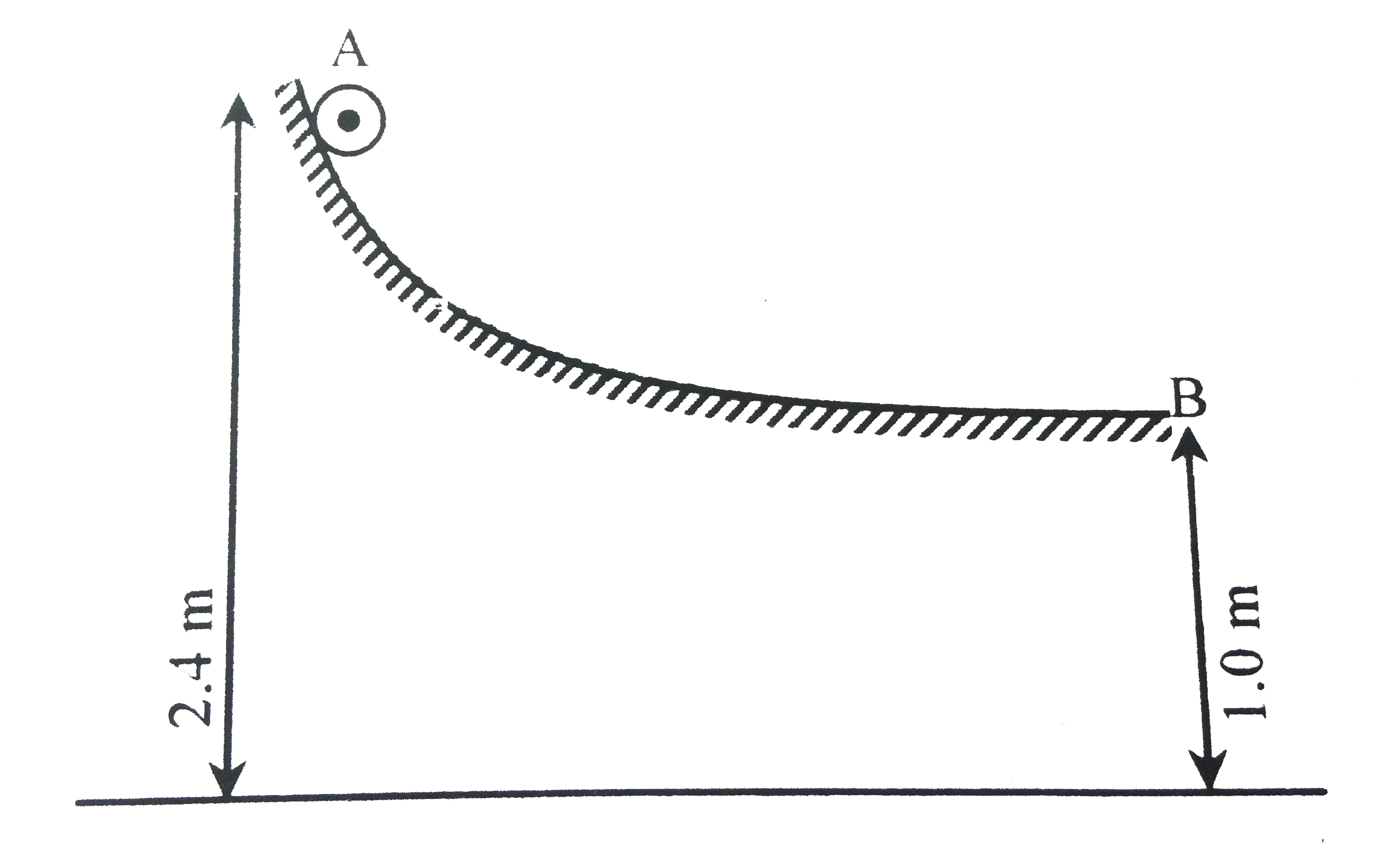 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionA monkey a mass 15 kg is climbing on a rope with one end fixed to the ceiling. If it whishes to go up with an acceleration of 1ms2, how much force should it apply to the rope? If the rope is 5 m long and the monkey starts from rest, how much time will it take to reach the ceiling?
View Solution
