An ellips inscribed in a semi-cicle touches the cicular are at two distinct points and also touches the bounding diameter. Its major axis is parallel to the bounding diameter. When the ellipse has the maximum passible area, its eccentricity is -
1√2
12
1√3
√23
The correct Answer is:D
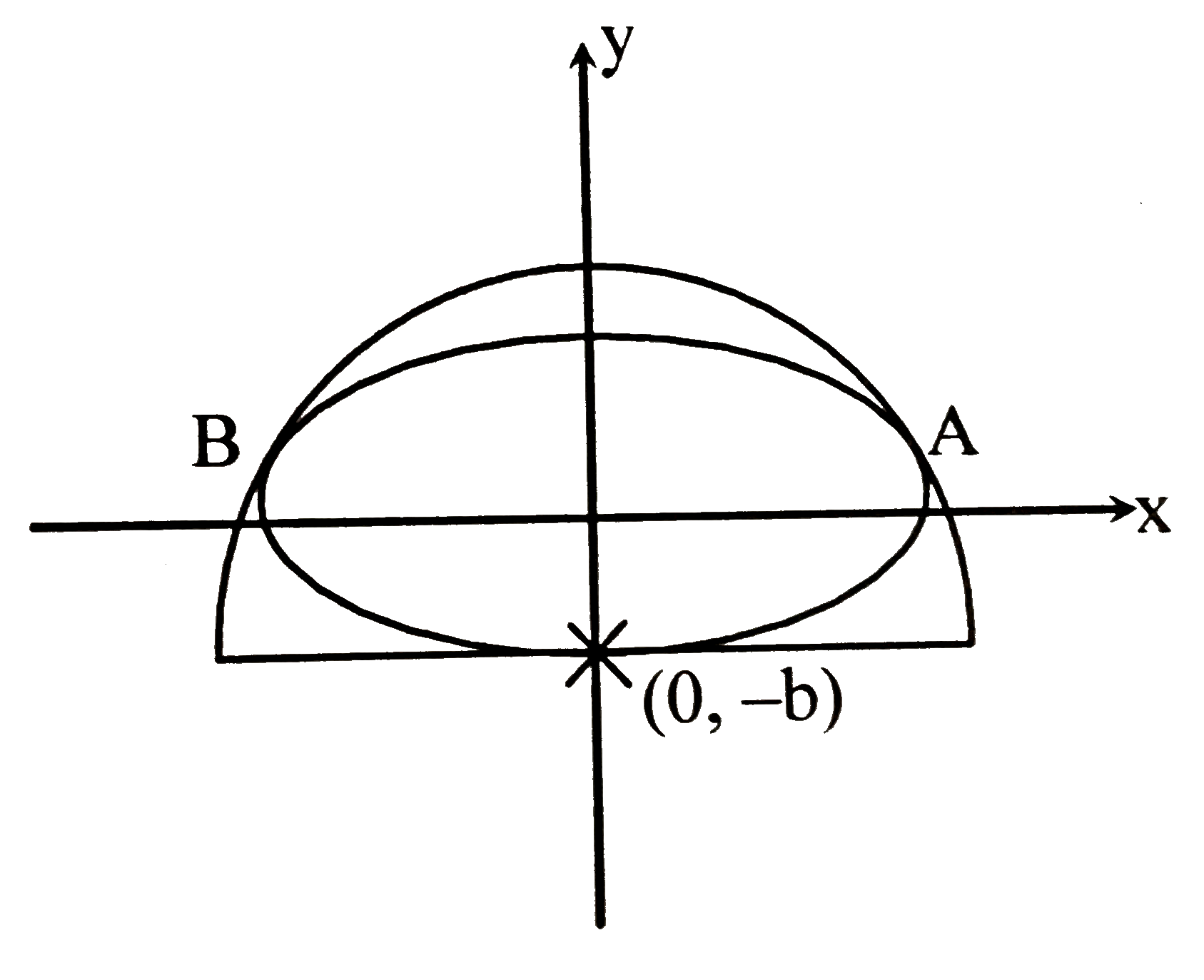
Let ellipse x2a2+y2b2=1
and circle x2+(y+b)2=r2 { let radius=2}
put x2−a2−a2y2b2
in circle a−a2y2b2+(y+b)2=r2
⇒(1−a2b2)y2+2by+(a2+b2−r2)=0
D=0⇒r2=a2a2−b2
⇒b=a√1−a2r2
Area =Δ=πab=πa2√1−a2r2
dΔda=0⇒a2=2r23⇒a=√23r
∴b=a√1−23=a√3⇒e=√23
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part B- Mathematics
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART -I MATHEMATICS
20 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
View SolutionAn ellipse has its centre at (1,−1) and semi-major axis = 8, which passes through the point (1,3).If the major axes is parallel to x-axis then the equation of ellipse is
View Solution
Knowledge Check
Let A and B be two distinct points on the parabola y2=4x. If the axis of the parabola touches a circle of radius r having AB as its diameter, then the slope of the line joining A and B can be
A−1/rB1/rC2/rD−2/rLet AandB be two distinct points on the parabola y2=4x. If the axis of the parabola touches a circle of radius r having AB as its diameter, then the slope of the line joining AandB can be (A) −1r (B) 1r (C) 2r (D) −2r
A−1/rB1/rC2/rD−2/rAn ellipse is drawn by taking a diameter of the circle (x–1)2+y2=1, as its semi-minor axis and a diameter of the circle x2+(y–2)2=4 as its semi-major axis. If the centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is:
A4x2+y2=8Bx2+4y2=16C4x2+y2=4Dx2+4y2=8
An ellipse has a centre at (1-1), and semimajor axis =8 and which passes through the point (1,3) . If the major axis is parallel to x-axis then the length of its latus rectum then find t4.
View SolutionA rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of rectangle so that the area is maximum. Find the area also.
View SolutionIf a triangle is inscribed in a n ellipse and two of its sides are parallel to the given straight lines, then prove that the third side touches the fixed ellipse.
View SolutionLet A and B be two distinct points on the parabola y2=4x. If the axis of the parabola touches a circle of radius r having AB as its diameter, then the slope of the line joining A and B can be
View SolutionA circle is inscribed in a trapezium in which one of the non-parallel sides is perpendicular to the two parallel sides. Then A) the diameter of the inscribed circle is the geometric mean of the lengths of the parallel sides B) the diameter of the inscribed circle is the harmonic mean of the lengths of the parallel sides C) the area of the trapezium is the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium D) the area of the trapezium is half the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium
View Solution
