An ellipse circumscribes a quadrilateral whose sides are given by x=−+2andy=±4. If the distance between focis is 4√6 and major axis is along yaxis then find the eqution of ellipse
The correct Answer is:x28+y232=1
Let the required ellipse be x2a2+y2b2=1
where a2=b2(1−e2).
Ellipse passes through the point (2,4)
∴4a2+16b2
Also, distance between foci is 4√6.
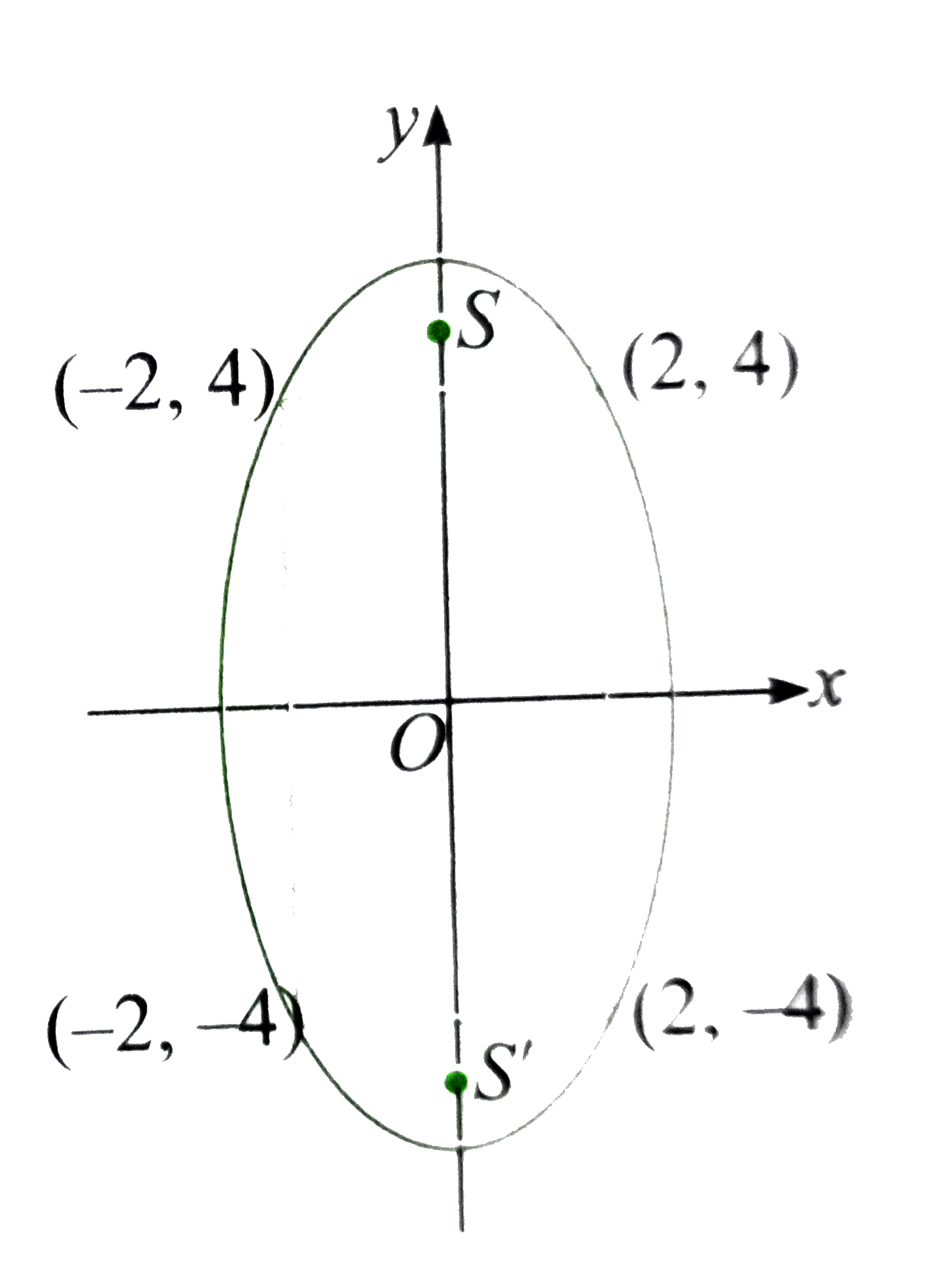
∴be=2√6
∴4b2−24+16b2=1
⇒rb4−44b2+16×24=0
⇒(b2−32)(b2−12)=0
∴b2=32(asb>4)
and a2=8
therefore, the requiredis x28+y232=1
Similar Questions
If the distance between the foci of an ellipse is equal to length of minor axis, then its eccentricity is
View SolutionIf the length of the latus rectum of an ellipse with major axis along x-axis and centre at origin is 20 units, distance between foci is equal to length of minor axis, then find the equation of the ellipse.
View Solution
Knowledge Check
In an ellipse the distance between the foci is 8 and the distance between the directrices is 25. The length of major axis, is
A10√2B20√2C30√2Dnone of theseLet the length of the latus rectum of an ellipse with its major axis along x-axis and centre at the origin be 8. If the distance between the foci of this ellipse is equal to the length of its minor axis, then which one of the following points lie on it
A(4√2,2√2)B(4√3,2√2)C(4√2,2√3)D(4√2,2√5)
If the focal distance of one ed of minor axis of an ellipse is k and distance betwnn foci is 2h then find the equation of the ellipse.
View SolutionIf the distance between the directrices is thrice the distance between the foci, then find eccentricity of the ellipse.
View SolutionThe eccentricity of an ellipse is 12 and the distance between its foci is 4 units. If the major and minor axes of the ellipse are respectively along the xandy axes, find the equation of the ellipse.
View SolutionThe eccentricity of an ellipse is 12 and the distance between its foci is 4 units. If the major and minor axes of the ellipse are respectively along the xandy axes, find the equation of the ellipse
View SolutionIf the length of the latus rectum of an ellipse with major axis along y-axis and centre at origin is 6 units, distance between foci is equal to length of minor axis, then the equation of the ellipse.
View SolutionIf the Latusrectum of an ellipse with axis along x- axis and centre at origin is 10 distance between foci=length of minor axis then the equation of the ellipse is
View Solution
