An ellipse has $O B$ as the semi-minor axis, $F a n d F'$ as its foci, and $∠ F B F'$ a right angle. Then, find the eccentricity of the ellipse.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{\sqrt{2}}$

$m_{B F} \cdot m_{B F} \equiv 1$
or $\frac{b - 0}{0 - a e} \times \frac{b - 0}{0 + a e} = 1$
or $\frac{b^{2}}{a^{2} e^{2}} = 1$
or $e^{2} = 1 - \frac{b^{2}}{a^{2} = 1 - e^{2}}$
or $e^{2} = \frac{1}{2}$
$e = \frac{1}{\sqrt{2}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

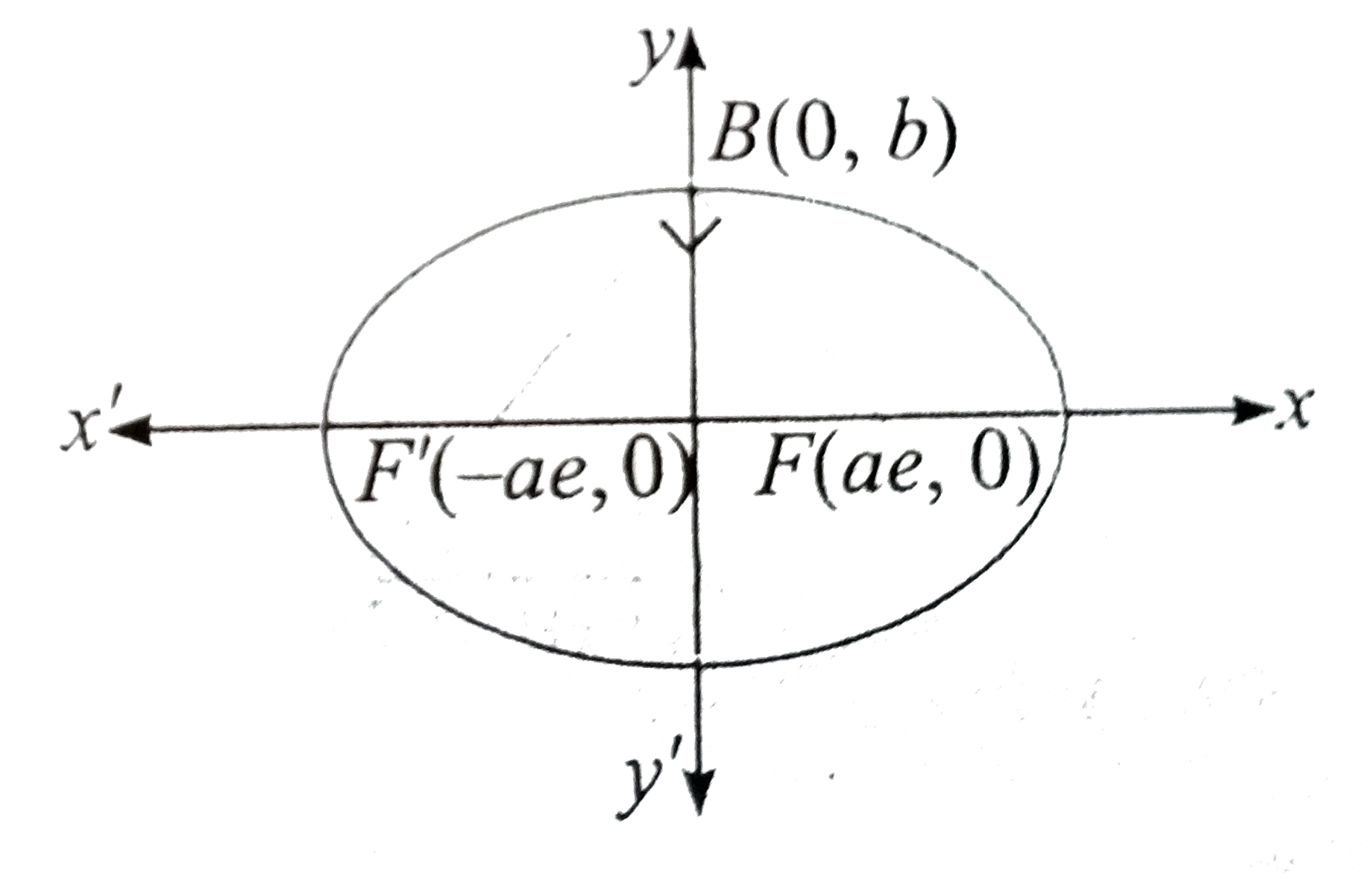
Similar Questions

Knowledge Check

Question 1 - Select One
An ellipse has $O B$ as the semi-minor axis, $F a n d F'$ as its foci, and $∠ F B F'$ a right angle. Then, find the eccentricity of the ellipse.
A $\frac{1}{4}$
B $\frac{1}{\sqrt{3}}$
C $\frac{1}{\sqrt{2}}$
D $\frac{1}{2}$
Question 2 - Select One
An ellipse has $O B$ as the semi-minor axis, $F a n d F'$ as its foci, and $∠ F B F'$ a right angle. Then, find the eccentricity of the ellipse.
A $\frac{1}{\sqrt{3}}$
B $\frac{1}{\sqrt{2}}$
C $\frac{1}{2}$
Dnone
Question 3 - Select One
An ellipse has $O B$ as the semi-minor axis, $F a n d F'$ as its foci, and $∠ F B F'$ a right angle. Then, find the eccentricity of the ellipse.
A $\frac{1}{2}$
B $\frac{1}{4}$
C $\frac{1}{\sqrt{2}}$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile