An equilateral triangle has side length 8. The area of the region containing all points outside the triangle but not more than 3 units from a point on the triangle is :
The correct Answer is:A
To find the area of the region containing all points outside an equilateral triangle of side length 8 but not more than 3 units from a point on the triangle, we can break the problem into several steps.
Step 1: Calculate the area of the equilateral triangle.
The formula for the area A of an equilateral triangle with side length a is given by:
A=√34a2
Substituting a=8:
A=√34×82=√34×64=16√3
Step 2: Determine the area of the rectangles formed outside the triangle.
Each side of the triangle will have a rectangle extending outward with a width of 3 units. The length of each rectangle is equal to the length of the side of the triangle, which is 8.
The area Ar of one rectangle is:
Ar=length×width=8×3=24
Since there are 3 sides to the triangle, the total area of the rectangles Arect is:
Arect=3×Ar=3×24=72
Step 3: Calculate the area of the sectors formed at each vertex.
At each vertex of the triangle, there is a sector of a circle with a radius of 3 units and a central angle of 120∘ (since the angles of an equilateral triangle are 60∘ each, and the external angle is 120∘).
The area As of one sector is given by the formula:
As=θ360∘×πr2
Substituting θ=120∘ and r=3:
As=120360×π×32=13×π×9=3π
Since there are 3 vertices, the total area of the sectors Asector is:
Asector=3×As=3×3π=9π
Step 4: Combine the areas to find the final answer.
The total area of the region outside the triangle but within 3 units from it is the sum of the area of the rectangles and the area of the sectors:
Total Area=Arect+Asector=72+9π
Thus, the area of the region containing all points outside the triangle but not more than 3 units from a point on the triangle is:
Total Area=72+9π
Final Answer:
The area of the region is 72+9π.
---
The formula for the area A of an equilateral triangle with side length a is given by:
Each side of the triangle will have a rectangle extending outward with a width of 3 units. The length of each rectangle is equal to the length of the side of the triangle, which is 8.
At each vertex of the triangle, there is a sector of a circle with a radius of 3 units and a central angle of 120∘ (since the angles of an equilateral triangle are 60∘ each, and the external angle is 120∘).
The total area of the region outside the triangle but within 3 units from it is the sum of the area of the rectangles and the area of the sectors:
The area of the region is 72+9π.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (More Than One Correct Option Type Questions)
20 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise For Session 11
10 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
9 Videos
Similar Questions
(c) 103 (d) 10 18. A circle is inscribed in an equilateral triangle with side lengths 6 unit. Another circle is drawn inside the triangle (but outside the first circle), tangent to the first circle and two of the sides of the triangle. The radius of the smaller circle is (b) 2/3 (a) 1/ root3 (c) 2 (d) 1
View SolutionThree point charges q are placed on vertices of an equilateral triangle of side length a. The charge Q that should be kept at centroid of triangle such that the system is in equilibrium is equal to
View Solution
Knowledge Check
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3
An equilateral triangle is inscribed in a circle. If a side of the triangle is 12 cm. If a side of the triangle is 12 cm. Find the area of the circle.
View SolutionSides AB and AC in an equilateral triangle ABC with side length 3 is extended to form two rays from point A as shown in the figure. Point P is chosen outside the triangle ABC and between the two rays such that ∠ABP+∠BCP=180∘. If the maximum length of CP is M, then M2/2 is equal to :
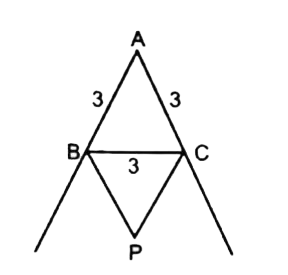
View SolutionOne side of an equilateral triangle is 18 cm. The mid-point of its sides are joined to form another triangle whose mid-points, in turn, are joined to form still another triangle. The process is continued indefinitely. Find the sum of the (i) perimeters of all the triangles. (ii) areas of all triangles.
View SolutionIf each side of an equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionIn an equilateral triangle with side a, prove that the altitude is of length a√32
View SolutionEquation of the base of an equilateral triangle is 3x+4y=9 and its vertex is at point (1,2) .Find the equations of the other sides and the length of each side of the triangle .
View Solution
