An equilateral triangle is inscribed in an ellipse whose equation is x2+4y2=4 If one vertex of the triangle is (0,1) then the length of each side is
8√313
24√313
16√313
48√313
The correct Answer is:C
We have x24+y2=1 (1)
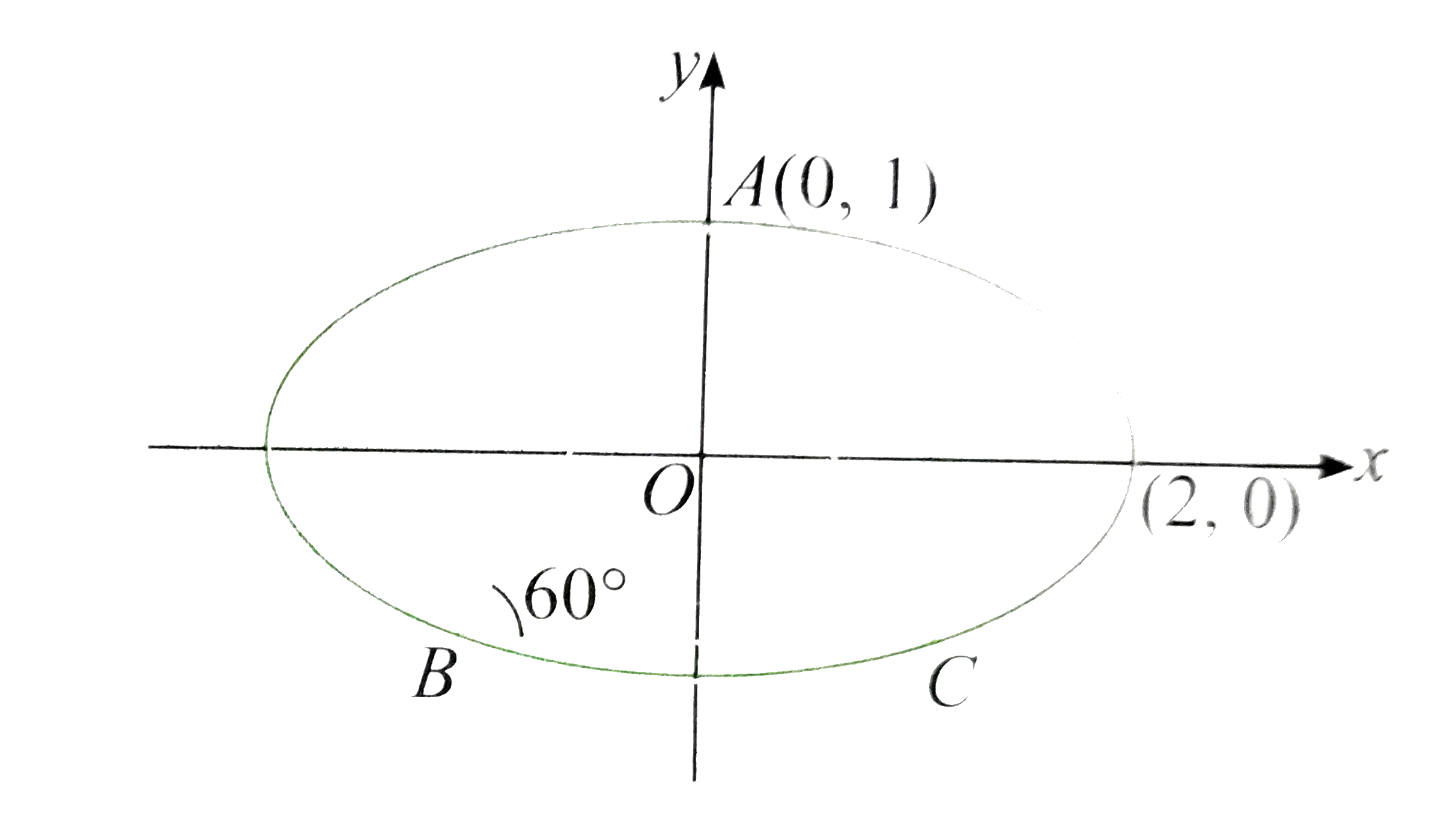
Equation of the sides AB is
y−1=√3(x−0)
⇒y=√3x+1 (2)
Solving (1) and (2), we get
x24+(√3x+1)2=1
⇒x2+4(3x2+1+2√3x)=4
⇒13x2+8√3x=0
rArx=0orx=−8√313
Putting x=−8√313 in (2), we get
y=−√3(8√313)+1=1−2413=−1113
Hence, B≡(8√313,1113)
∴C≡(8√313,1113)
∴BC≡16√313
Similar Questions
An equilateral triangle is inscribed in the ellipse whose equation is x2+4y2=4. One vertex of the triangle (0, 1) and one altitude is contained in the y - axis. If the length of each side is k√3 units, then k is
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose vertex is at the vertex of the parabola .Find the length of its side.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, such that one vertex of this triangle coincides with the vertex of the parabola. Then find the side length of this triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, such that one vertex of this triangle coincides with the vertex of the parabola. Then find the side length of this triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose vertex is at of the parabola. Find the length of its side.
View SolutionAn equilateral trinalge is inscribed in the parabola y2=−8x, where one vertex is at the vertex of the parabola. Find the length of the side of the tringle.
View SolutionIf an equilateral triangle is inscribed in the circle x2+y2=a2, the length of its each side is
View SolutionIf one vertex of an equilateral triangle is at (2.−1) 1base is x+y−2=0, then the length of each side, is
View SolutionEquation of the base of an equilateral triangle is 3x+4y=9 and its vertex is at point (1,2) .Find the equations of the other sides and the length of each side of the triangle .
View Solution

