An equilateral triangle is inscribed in an ellipse whose equation is x2+4y2=4 If one vertex of the triangle is (0,1) then the length of each side isSolution in Bengali
8√313
24√313
16√313
48√313
The correct Answer is:C
We have x24+y2=1 (1)
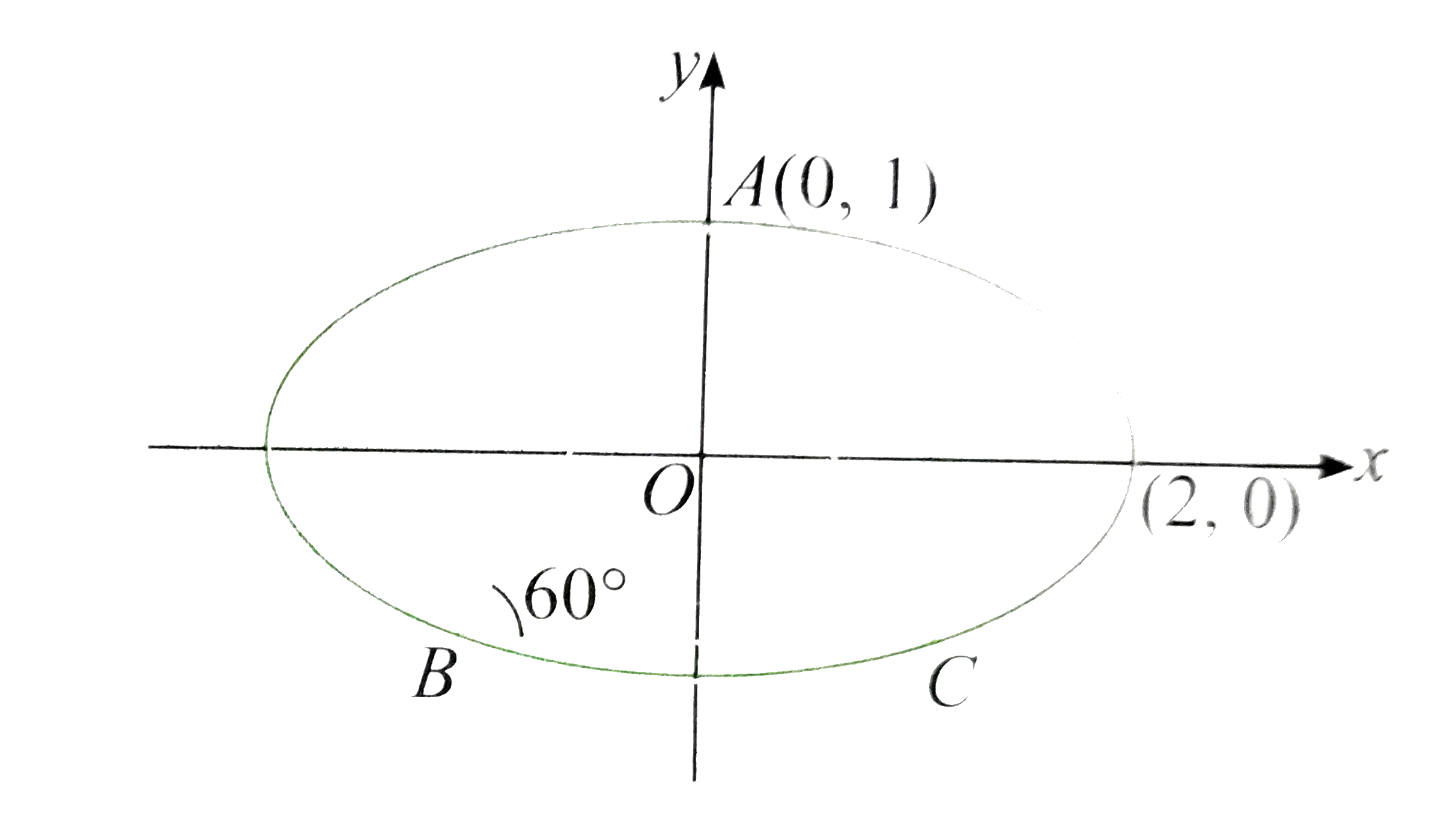
Equation of the sides AB is
y−1=√3(x−0)
⇒y=√3x+1 (2)
Solving (1) and (2), we get
x24+(√3x+1)2=1
⇒x2+4(3x2+1+2√3x)=4
⇒13x2+8√3x=0
rArx=0orx=−8√313
Putting x=−8√313 in (2), we get
y=−√3(8√313)+1=1−2413=−1113
Hence, B≡(8√313,1113)
∴C≡(8√313,1113)
∴BC≡16√313
Similar Questions
An equilateral triangle is inscribed in the parabola y2=4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View SolutionAn equilateral triangle is Inscribed in parabola y2=4ax whose one vertex is at origin then length of side of triangle
View SolutionAn equilateral triangle is inscribed in an ellipse whose equation is x2+4y2=4 If one vertex of the triangle is (0,1) then the length of each side is
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose one vertex is at the vertex of the parabola
if 1 cms is the side of the equilateral triangle prove that the length of each altitude of the triangle is 1√32cms
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View Solution
