An equilateral triangle is inscribed in the parabola y2=4ax where are at the vertex of the parabola. find the length of the side of the triangle.
8√3a
8√2a
4√3a
4√2a
The correct Answer is:A
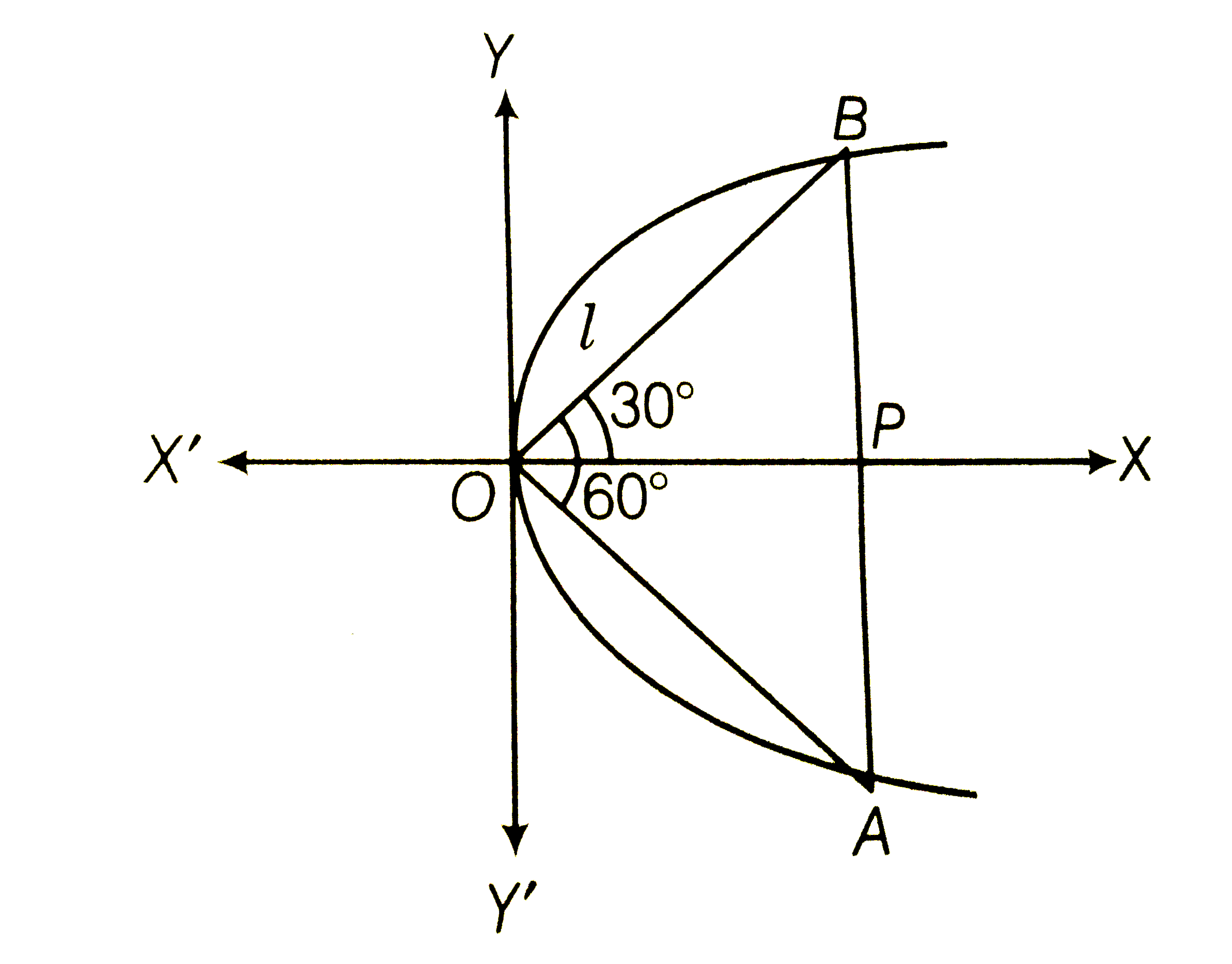
First, we draw the parabola in the positive side of X-axis and inside that, draw an equilaaterl Δoab. let OB =1=OA=AB ∠BOA=60∘⇒∠BOP=30∘ in ΔBOP
sin30∘=pbob ⇒12=OP1⇒PB=12
andcos30∘=OPOB
⇒√32=op1⇒op=1√32
∴ coordinates of B=(OP,PB)=( (√(1)2,12)willsatiyy^2=4ax<br>(1/2)^(2)=(4axx1)/sqrt3(2)<br>rArr (1^2)/(1)=(4al)sqrt3/(2) ⇒1=8√3a
Topper's Solved these Questions
Similar Questions
An equilateral triangle is inscribed in the parabola y2=4ax where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose vertex is at the vertex of the parabola. The length of its side is
View Solution
Knowledge Check
If OAB is an equilateral triangle inscribed in the parabola y2=4ax with O as the vertex, then the length of the side of △OAB is
A8a√3B4a√3C2a√3Da√3If OAB is an equilateral triangle inscribed in the parabola y2=4ax with O as the vertex, then the length of the side of the ΔOAB is
A8a√3B4a√3C2a√3Da√3An equilateral trinagle is inscribed in parabola y2=8x whose one vertex coincides with vertex of parabola.Find area of triangle.
A(196√3)B(194√3)C(192√3)D(190√3)
An equilateral trinalge is inscribed in the parabola y2=−8x, where one vertex is at the vertex of the parabola. Find the length of the side of the tringle.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax whose vertex is at of the parabola. Find the length of its side.
View SolutionAn equilateral triangle is inscribed in the parabola y2=4ax, such that one vertex of this triangle coincides with the vertex of the parabola. Then find the side length of this triangle.
View SolutionIf an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height
View SolutionIf an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height is
View Solution
