An investigator interviewed 100 students to determine their preferences for the three drinks, milk (M), coffee (C ) and tea (T). He reported the following: 10 students has all three drinks M, C, T, 20 had M and C, 30 had C and T, 25 had M and T, 12 had M only, 5 had C only and 8 had T only. Using a Venn diagram, find how many did not take any of the three drinks? Solution in Punjabi
Given, M, C and T are the sets of drinks, milk, coffee and tea, respectively. Let us denote the number of drinks (students) contained in the bounded region as shown in the diagram by a, b, c, d, e, f and g, respectively.
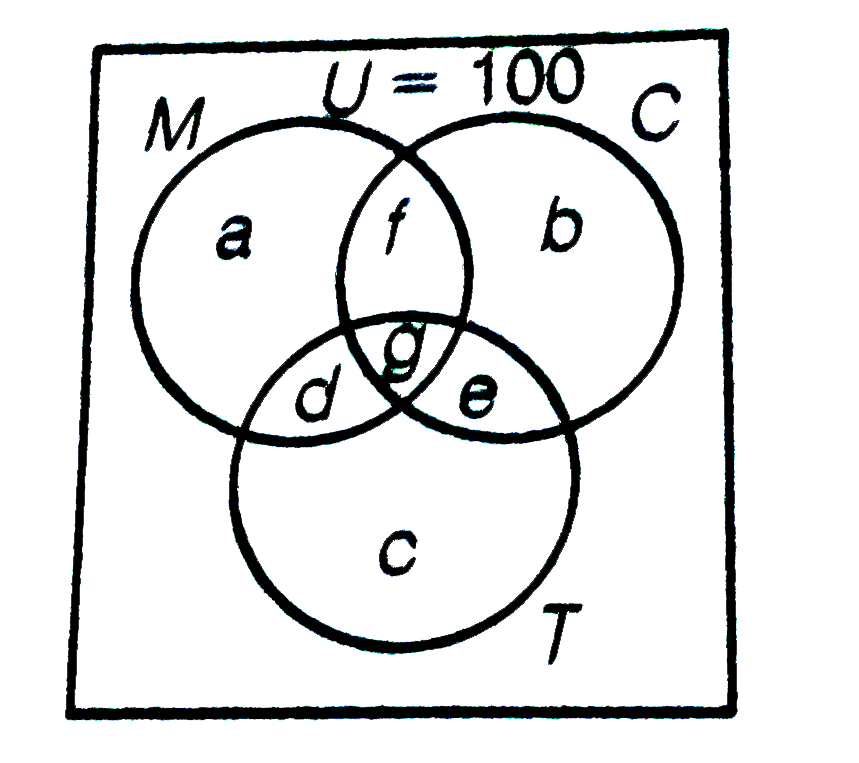
Then, g = 10
g + f = 20 implies f = 10 [∵g=10]
g + e = 30 implies e = 20
d + g = 25 implies d = 15
and a = 12, b = 5, c = 8
Thus, total number of students taking drinks M or C or T
= a + b + c + d + e + f + g
= 12 + 5 + 8 + 15 + 20 + 10 + 10 = 80
Hence, the number of students taking none of them drinks
= 100 - 80 = 20
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 1
11 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 2
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
Similar Questions
If X={4n−3n−1:n∈N}andy={9(n−1):n∈N}, then X∪Y equals
View SolutionIf A = {2, 3, 5}, B = {2, 5, 6}, then (A−B)×(A∩B) is
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionAn investigator interviewed 100 students to determine the performance of three drinks: that 10 students take all three drinks milk, milk, coffee and tea. The investigator reported coffee and tea; 20 students take milk and coffee: 25 students take milk and tea; 20 students take coffee and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. then the number of students who did not take any of three drinks is
View SolutionIn the cinema set of a movie, 125 mechanical aliens were created. Some of these aliens had peculiar features. 40 had two noses, 30 had three legs, 20 had four ears, 10 had two noses and three legs, 12 had three legs and four ears, 5 had two noses and four ears and 3 had all the three unusual features. How many were there without any of these unusual features? (a) 5 (b) 35 (c) 80 (d) None of these
View SolutionAn lnvestigator interviewed 100 students to determine the performance of three drinks milk, coffee and tea. The investigator reported that 10 students take all three drinks, 20 students take milk and coffee, 30 students take coffee and tea, 25 students take milk and tea, 12 studnts take milk only. 5 students take coffee only and 8 student take tea only. Then the number of students who did not take any of the three drinks is λ . The value of λ4 is equal to
View SolutionIn a survey of 25 students, it was found that 15 had taken Mathematics, 12 had taken Physics and 11 had taken Chemistry, 5 had taken Mathematics and Chemistry, 9 had taken Mathematics and Physics, 4 had taken Physics and Chemistry and 3 had taken all the three subjects.
Consider the following statements :
1. The number of students who had taken only one subject is equal to the number of students who had taken only two subjects.
2. The number of students who had taken at least two subjects is four times the number of students who had taken all the three subjects.
Which of the above statements is/are correct ?
View Solutionएक अनुसंधानकर्त्ता ने तीन पेयों :दूध (M), कॉफ़ी (C) और चाय (T) की वरीयता जानने के लिए 100 विद्यार्थियों का साक्षात्कार लिया। उन्होंने सूचित किया की 10 विद्यार्थी तीनों पेय M,C,T, 20M और C, 30C और T,25M और T, 12 केवल M, 5 केवल C, 8 केवल T लिया तथा। वेन आरेखा के प्रयोग से ज्ञात कीजिए की कितने विद्यार्थियों ने तीनों में से कोई नहीं लिया ?
View Solution25 विद्यार्थियों के सर्वेक्षण में यह पाया गया की 15 विद्यार्थियों ने गणित लिया तथा, 12 विद्यार्थियों ने भौतिकी लिया था, 11 विद्यार्थियों ने केमिस्ट्री लिया था, 5 विद्यार्थियों ने गणित और केमिस्ट्री लिया था, 9 विद्यार्थियों ने गणित और भौतिकी लिया था, 4 विद्यार्थियों ने भौतिकी और केमिस्ट्री लिया था, और 3 विद्यार्थियों ने सभी विषयों को लिया था। उन विद्यार्थियों की संख्या ज्ञात कीजिए जो लिए थे- (i) केवल केमिस्ट्री (ii) केवल गणित (iii) केवल भौतिकी (iv) भौतिकी और केमिस्ट्री लेकिन गणित नहीं (v) गणित और भौतिकी किन्तु केमिस्ट्री नहीं (vi) विषयों में केवल एक (vii) कम-से-कम तीनों विषय (viii) तीनों विषयों में से कोई नहीं।
View Solution100 विघार्थियों के समूह में तीन पेयों - दूध (M), कॉफी (C) एवं चाय (T) - में से कौन क्या पीता है इसके बारे में एक अन्वेषक निम्नलिखित तथ्य प्राप करता है-
10 विघार्थी सभी प्रकार के पेय M, C और T लेते है, 20 M और C लेते है, 30 C और T लेते है, 25 M और T लेते है, 12 केवल M, 5 केवल C एवं 8 केवल T लेते है| बताएँ उनमे से कितनों ने एक भी पेय नहीं लिया|
View SolutionAn investigator interviewed 100 students to determine the performance of three drinks: milk , coffee and tea the in vestigotor reported that 10 students take all three drinks milk . Coffe and tea , 20 students take take coffe , 25 students take milk only , 5 students take coffee only and 8 students take tea only . then the number of students who did not take any of these drinks is
View SolutionAn investigator interviewed 100 students to determine their preferences for the three drinks : milk (M) , coffee (C ) and tea (T) . He reported the following : 10 students had all the three drinks M, C, T , 20 had M and C only , 30 had C and T , 25 had M and T , 12 had M only , 5 had C only , 8 had T only . Find how many did not take any of the three drinks
View SolutionQ.N. 45 In a survey of 25 students ,it was found that 15 had taken mathematics , 12 had taken physics and 11 had taken chemistry ,5 had taken mathematics and chemistry, 9 had taken mathematics and physics, 4 had taken physics and chemistry and 3 had taken all the three subjects. write the number of student that had taken (a) at least one of three subjects (b) only mathematics
View SolutionAn investigator interviewed 100 students to determine the performance of three drinks: that 10 students take all three drinks milk, milk, coffee and tea. The investigator reported coffee and tea; 20 students take milk and coffee: 25 students take milk and tea; 20 students take coffee and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. then the number of students who did not take any of three drinks is
View Solutionदो संख्याओं का म. स. यदि उनमें से ही एक संख्या उनका ल. स. दूसरी संख्या होगा|
View Solution
