An object moves in a straight line with deceleration whose magnitude varies with velocity s 3v23. If at an initial point, the velocity is 8/m sec, then the distance travelled by the object before it stops is
2m
4m
6m
8m
The correct Answer is:B
V0=8m/sec
ds=−V2−02a=−(8)22(9.8)=3.265
∴ds≈4m
Topper's Solved these Questions
- BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry18videos
EAMCET - 2018 (TS) SHIFT - 2
- BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry18videos
EAMCET - 2018 (TS) SHIFT - 2
- BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 1EXERCISE - EXERCISE - Chemistry8videos
EAMCET - 2018 (TS) SHIFT - 1
- BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY3videos
EAMCET -2016 (AP)
Similar Questions
An object Is vertically projected with an initial velocity of 20ms−1.Calculate the distance travelled by the object in 3 seconds.(g=10ms−2)
View SolutionA particle starts from rest and moves along a straight line such that its acceleration a as a function of velocity v is given as a=(5)/(3v+2) where a is in m/s^(2) and v is in m/s .The distance travelled by the particle till it attains velocity of 10m/s is
View Solution
Knowledge Check
- Question 1 - Select One
If a body moving with an initial velocity of 3 m/s and an acceleration of 2m/s2. Then what will be the distance travelled by the body in 4th second.
A6 mB7 mC10 mD28 m - Question 2 - Select One
The velocity versus time graph of a body moving in a straight line is as follows. The distance travelled by the body is 5 sec is
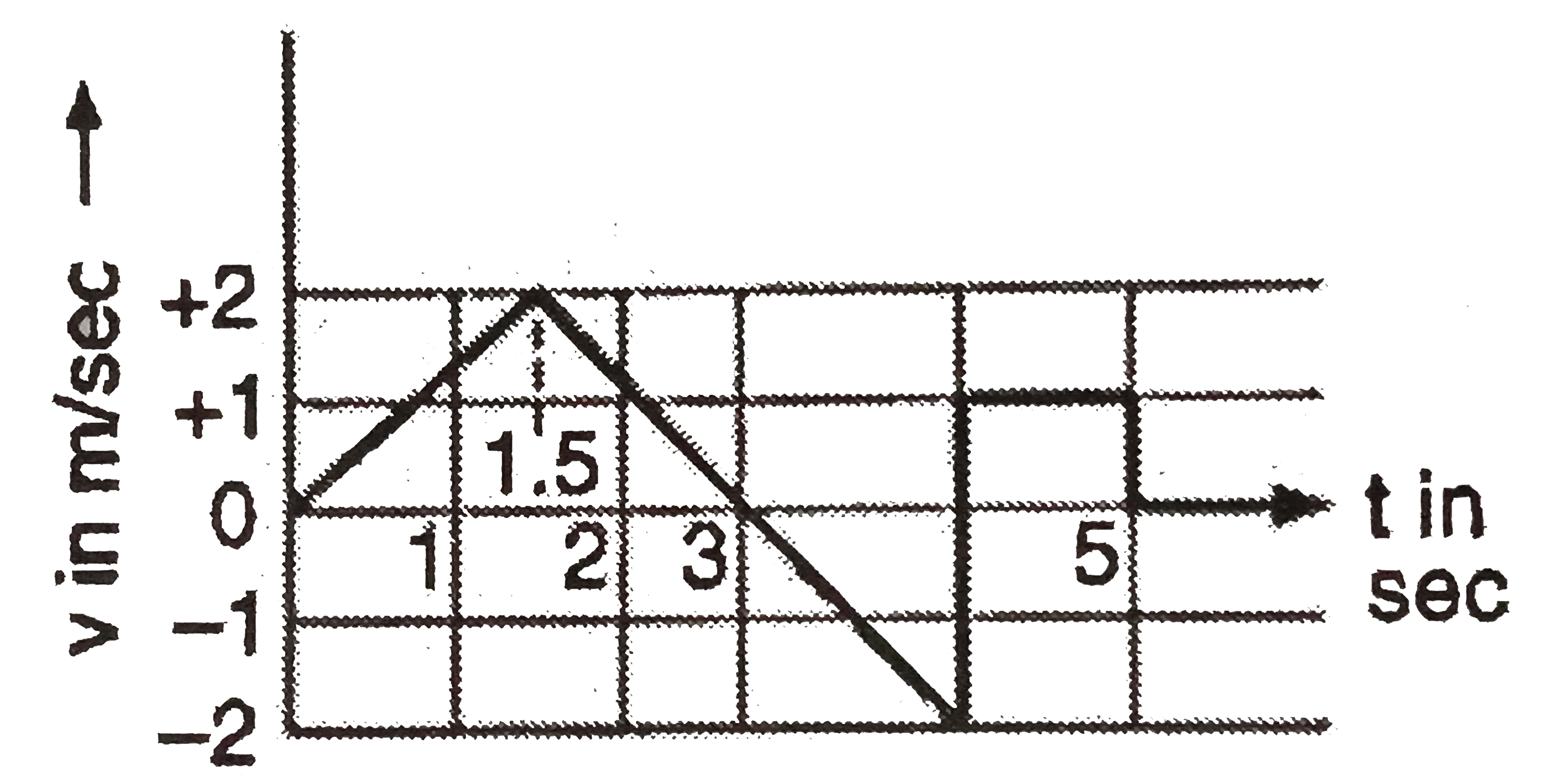 A2 mB3 mC4 mD5 m
A2 mB3 mC4 mD5 m - Question 3 - Select One
A particle travels A to M along a straight line with a velocity of 8 m/s and M to A with a velocity of 2 m/s,
then the average velocity for the whole journey is –A3.2 m/sB−5m/sC−3.3m/sD0 m/s
A particle is moving along a straight line with uniform retardation of 2ms−2 The initial speed of particle is 20m/s .The distance travelled by the particle during the last one second before it stops is
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as α=k√v, where k is a positive constant. At the initial moment the velocity of the point is equal to V0. What distance will it take to cover that distance?
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as w=a√v, where a is a positive constant. At the initial moment the velocity of the point is equal to v0. What distance will it traverse before it stops? What time will it take to cover that distance?
View SolutionA particle moves on a straight line with velocity 2 m/s covers a distance of 5 m, returns back to initial position along same path with velocity 4 m/s. The distance and displacement covered by particle are respectively.
View SolutionA particle moves on a straight line with velocity 2 m/s covers a distance of 5 m, returns back to initial position along same path with velocity 4 m/s. The distance and displacement covered by particle are respectively.
View Solution

