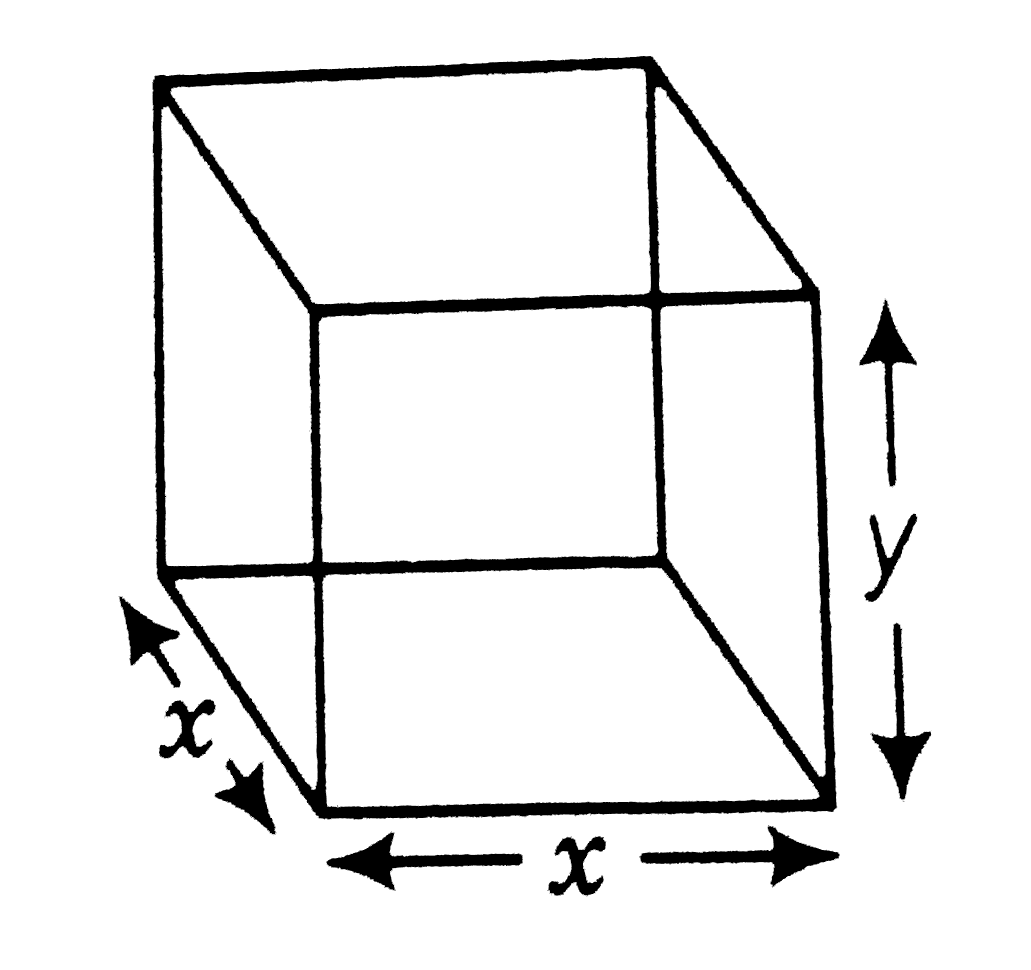
An open box with a square base is to be made out of a given quantity of card board of area $c^{2}$ square units. Show that the maximum volume of the box is $\frac{c^{3}}{6 \sqrt{3}}$ cubic units.

Video Solution

Text Solution

Verified by Experts

Let the length of the square base of open box be x unit and is height be y units.
$∴$ Area of the metal used $= x^{2} + 4 x y$
$\Rightarrow y = \frac{c^{2} - x^{2}}{4 x}$ ……….(i) [given]
Now, volume of the box(V) = $x^{2} y$
$\Rightarrow V = x^{2} . \frac{c^{2} - x^{2}}{4 x}$
$= \frac{1}{4} x (c^{2} - x^{2})$
$= \frac{1}{4} (c^{2} x - x^{3})$

On differentiating both sides w.r.t. x, we get
$\frac{d V}{d x} = \frac{1}{4} (c^{2} - 3 x^{2})$ .............(ii)
Now, $\frac{d V}{d x} = 0 \Rightarrow c^{2} = 3 x^{2}$
$\Rightarrow x^{2} = \frac{c^{2}}{3}$
$\Rightarrow x^{2} = \frac{c^{2}}{3}$
$\Rightarrow x = \frac{c}{\sqrt{3}}$ [using positive sign]
Again, differentiating Eq. (ii) w.r.t. x, we get
$\frac{d^{2} v}{{({d x}^{2})}_{at x = \frac{c}{\sqrt{3}}}^{2}} = - \frac{3}{2} . (\frac{c}{\sqrt{3}}) < 0$
Thus, we see that volume (V) is maximum at $x = \frac{c}{\sqrt{3}}$ .
$∴$ Maximum volume of the box, ${(V)}_{x = \frac{c}{\sqrt{3}}} = \frac{1}{4} (c^{2} . \frac{c}{\sqrt{3}} - \frac{c^{3}}{3 \sqrt{3}})$
$= \frac{1}{4} . \frac{3 c^{3} - c^{3}}{3 \sqrt{3}} = \frac{1}{4} . \frac{2 c^{3}}{3 \sqrt{3}}$
$= \frac{c^{3}}{6 \sqrt{3}}$ cu units

Updated on:21/07/2023