An ordinary dice is rolled a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even numebr 3 times. Then the probability of getting an odd number and odd number of times, is
1/32
5/16
1/2
none of these
The correct Answer is:C
To solve the problem, we need to find the probability of getting an odd number an odd number of times when rolling a die a certain number of times, given that the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times.
1. Define the Problem:
We are rolling a die n times. The odd numbers on a die are 1, 3, and 5, which gives us a probability p=36=12 of rolling an odd number.
2. Set Up the Probabilities:
The probability of getting an odd number exactly r times in n rolls can be expressed using the binomial probability formula:
P(X=r)=(nr)pr(1−p)n−r
For our case, we need:
- Probability of getting an odd number 2 times:
P(X=2)=(n2)(12)2(12)n−2=(n2)(12)n
- Probability of getting an even number 3 times (which is equivalent to getting an odd number n−3 times):
P(X=n−3)=(n3)(12)3(12)n−3=(n3)(12)n
3. Set the Probabilities Equal:
Since the problem states that these two probabilities are equal:
(n2)(12)n=(n3)(12)n
We can cancel (12)n from both sides:
(n2)=(n3)
4. Use the Binomial Coefficient Identity:
The identity (nr)=(nn−r) implies that:
(n2)=(n3)⟹n−2=3⟹n=5
5. Calculate the Required Probability:
Now that we know n=5, we need to find the probability of getting an odd number an odd number of times (1, 3, or 5 times):
P(X=1)=(51)(12)5=5⋅132=532
P(X=3)=(53)(12)5=10⋅132=1032
P(X=5)=(55)(12)5=1⋅132=132
Now, we sum these probabilities:
P(odd number of times)=P(X=1)+P(X=3)+P(X=5)=532+1032+132=1632=12
Final Answer:
The probability of getting an odd number an odd number of times is 12.
We are rolling a die n times. The odd numbers on a die are 1, 3, and 5, which gives us a probability p=36=12 of rolling an odd number.
The probability of getting an odd number exactly r times in n rolls can be expressed using the binomial probability formula:
P(X=r)=(nr)pr(1−p)n−r
For our case, we need:
- Probability of getting an odd number 2 times:
P(X=2)=(n2)(12)2(12)n−2=(n2)(12)n
- Probability of getting an even number 3 times (which is equivalent to getting an odd number n−3 times):
P(X=n−3)=(n3)(12)3(12)n−3=(n3)(12)n
Since the problem states that these two probabilities are equal:
(n2)(12)n=(n3)(12)n
We can cancel (12)n from both sides:
(n2)=(n3)
The identity (nr)=(nn−r) implies that:
(n2)=(n3)⟹n−2=3⟹n=5
Now that we know n=5, we need to find the probability of getting an odd number an odd number of times (1, 3, or 5 times):
P(X=1)=(51)(12)5=5⋅132=532
P(X=3)=(53)(12)5=10⋅132=1032
P(X=5)=(55)(12)5=1⋅132=132
P(odd number of times)=P(X=1)+P(X=3)+P(X=5)=532+1032+132=1632=12
The probability of getting an odd number an odd number of times is 12.
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
A die is rolled n times. If the probability of getting odd number 2 times is equal to the probability of getting even number 3 times. Find the probability of getting odd number odd times
View SolutionA fair die is thrown n times. The probability of getting an odd number twice is equal to that getting an even number thrice. The probability of getting an odd number, odd number of times is
View Solution
Knowledge Check
An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is :
A132B516C316D12If an unbiased dice is rolled, then the probability of getting an even number is _______ then/to that of getting an odd number.
AMoreBLessCEqualDCannot sayA fair coin is tossed 100 times. What is the probability of getting tails an odd number of times?
A14B23C12D34
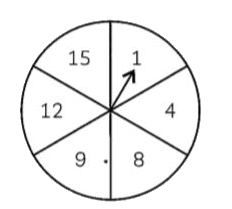
What is the probability of getting an odd number on the spinner?
View SolutionA die is thrown once. find the probability of getting an odd number
View SolutionA die is thrown once. Find the probability of getting an odd number.
View SolutionA fair coin is tossed 100 times the probability of getting tails an odd number of time is
View SolutionWhen a die is thrown, the probability of getting an odd number less than 3 is
View Solution
