Anjali places a mirror on level ground to determine the height of a tree (see the diagram) . She stands at a certain distance so that she can see the top of the tree reflected from the mirror . Anjali's eye level is 1.8 m above the ground . The distance of Anjali and the tree from the mirror are 1.5 m and 2.5 m respectively.
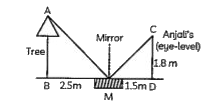
(i) Name the two similar triangles that are formed in the diagram.
ii. State the criterion of similarity that is applicable here.
iii. Find the height of the trees.
Step by step video & image solution for Anjali places a mirror on level ground to determine the height of a tree (see the diagram) . She stands at a certain distance so that she can see the top of the tree reflected from the mirror . Anjali's eye level is 1.8 m above the ground . The distance of Anjali and the tree from the mirror are 1.5 m and 2.5 m respectively. (i) Name the two similar triangles that are formed in the diagram. ii. State the criterion of similarity that is applicable here. iii. Find the height of the trees. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
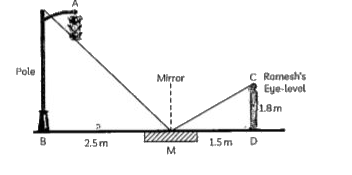
The two similar triangles shown in the figure are:View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
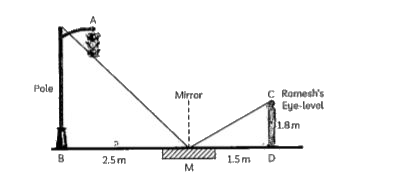
The height of the pole is:View Solution
Knowledge Check
- Question 1 - Select One
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
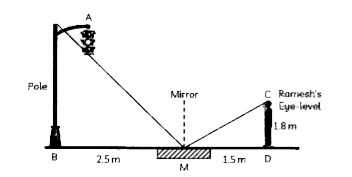
The height of the pole is:A3 metresB2.8 metresC3.2 metresD3.8 metres - Question 2 - Select One
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
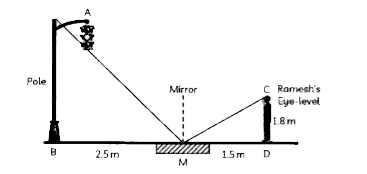
The two similar triangles shown in the figure are:AΔABM,ΔMCDBΔAMB,ΔCMDCΔABM,ΔCMDDΔABM,ΔMDC - Question 3 - Select One
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

Which criterion of similarity is applicable to similar triangles?ASSABASACSSSDAAA
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

Which criterion of similarity is applicable to similar triangles?View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
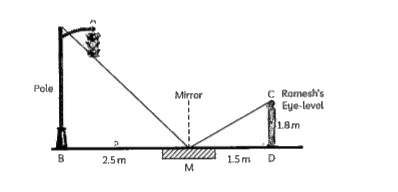
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:View Solution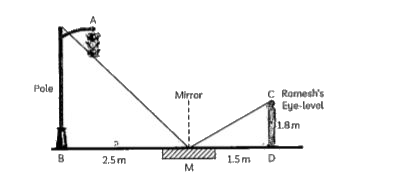
If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

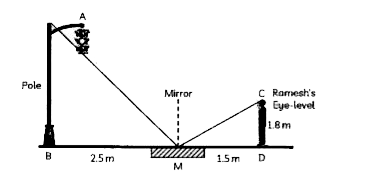
If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:View Solution

