Another name for the mean of a probability distribution is expected value.
To solve the question, we need to establish the relationship between the mean of a probability distribution and the expected value. Here’s a step-by-step solution:
Step 1: Understand the Mean of a Probability Distribution
The mean of a probability distribution, often denoted by μ, is a measure of the central tendency of the distribution. It represents the average value of a random variable.
Hint: The mean gives us an idea of where the center of the distribution lies.
Step 2: Define Expected Value
The expected value (denoted as E(X) or sometimes E(x)) of a random variable X is calculated using the formula:
E(X)=∑(x⋅P(x))
where x represents the possible values of the random variable and P(x) is the probability of each value.
Hint: The expected value is a weighted average where probabilities act as weights.
Step 3: Relate Mean and Expected Value
From the definition of expected value, we can see that the mean of a probability distribution can be expressed as:
μ=E(X)=∑(x⋅P(x))
This shows that the mean of a probability distribution is indeed the expected value of the random variable.
Hint: Look for the mathematical expressions that connect different concepts in probability.
Step 4: Conclusion
Since we have established that the mean of a probability distribution is equal to the expected value, we can conclude that the statement in the question is true.
Hint: Always summarize your findings to reinforce your understanding.
Final Answer:
The statement "Another name for the mean of a probability distribution is expected value" is true.
---
The mean of a probability distribution, often denoted by μ, is a measure of the central tendency of the distribution. It represents the average value of a random variable.
The expected value (denoted as E(X) or sometimes E(x)) of a random variable X is calculated using the formula:
From the definition of expected value, we can see that the mean of a probability distribution can be expressed as:
Since we have established that the mean of a probability distribution is equal to the expected value, we can conclude that the statement in the question is true.
The statement "Another name for the mean of a probability distribution is expected value" is true.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions38videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example101videos
MATRICES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers15videos
RELATIONS AND FUNCTIONS
Similar Questions
Find the mean of the following distribution :
 View Solution
View SolutionIf the mean of the following distribution is 3 find the value of p.
 View Solution
View SolutionFind the mean of the following distribution:
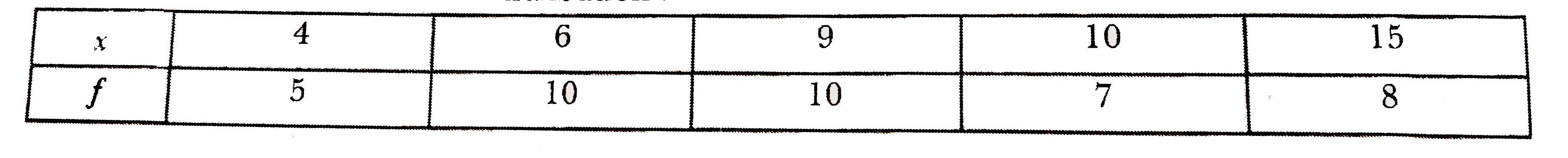 View Solution
View SolutionFind the mean of the following distribution:
 View Solution
View SolutionIf the mean of the following distribution is 6, find the value of p
View SolutionFor the following probability distribution.
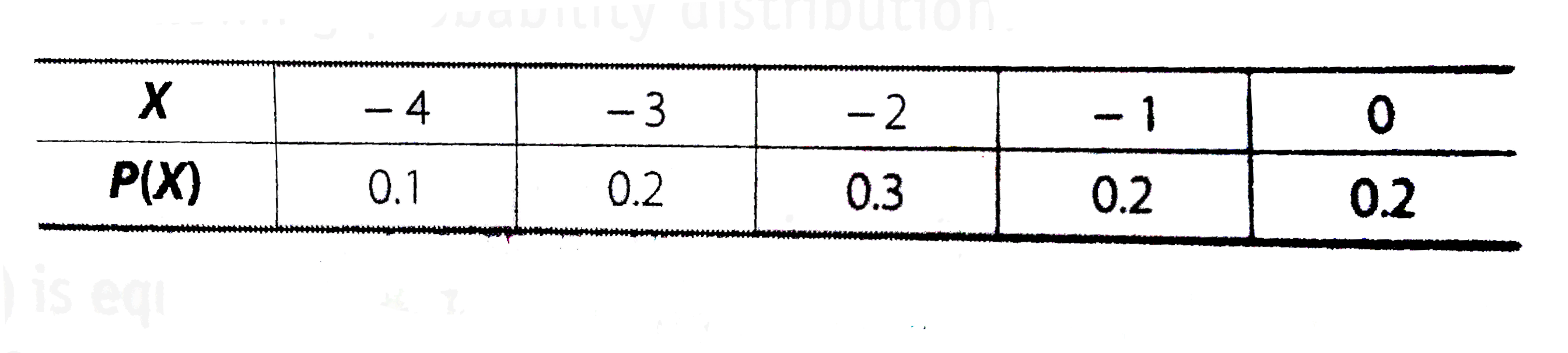
E(X) is equal toView SolutionIf the mean of the following distribution is 24, find the value of 'a'.
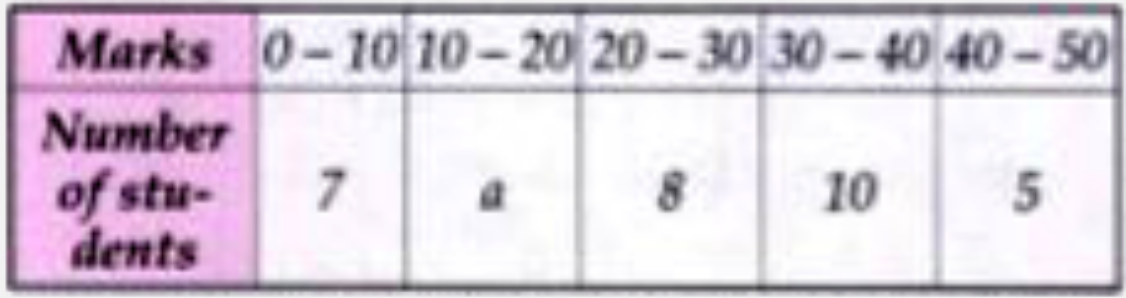 View Solution
View SolutionCalculate the mean of the following distribution :
 View Solution
View SolutionFind the value of p, if the mean of following distribution is 20.
 View Solution
View SolutionFind the value of if the mean of the following distribution is 7.5
View Solution

