Answer the following questions:
1. Define Constraints of LPP.
Step-by-Step Solution:
1. Definition of Constraints in Linear Programming Problems (LPP):
- Constraints in a linear programming problem refer to the limitations or restrictions placed on the variables involved in the problem. These constraints can be expressed as linear inequalities or equations.
2. Understanding the Nature of Constraints:
- Constraints dictate the feasible region where the solution to the linear programming problem can exist. They define the boundaries within which the variables must operate.
3. Types of Constraints:
- Constraints can be classified into different types:
- Inequality Constraints: These are expressed in the form of inequalities, such as ax+by≤c or ax+by≥d.
- Equality Constraints: These are expressed in the form of equalities, such as ax+by=c.
- Non-Negative Constraints: These specify that the variables cannot take negative values, such as x≥0 and y≥0.
4. Examples of Constraints:
- For example, if we have a linear programming problem with variables x and y, the constraints might include:
- x+2y≤10 (an inequality constraint)
- 3x+y=15 (an equality constraint)
- x≥0 and y≥0 (non-negative constraints)
5. Conclusion:
- In summary, constraints are essential components of linear programming problems that define the limitations on the variables. They help in determining the feasible solutions that satisfy all the given conditions.
- Constraints in a linear programming problem refer to the limitations or restrictions placed on the variables involved in the problem. These constraints can be expressed as linear inequalities or equations.
- Constraints dictate the feasible region where the solution to the linear programming problem can exist. They define the boundaries within which the variables must operate.
- Constraints can be classified into different types:
- Inequality Constraints: These are expressed in the form of inequalities, such as ax+by≤c or ax+by≥d.
- Equality Constraints: These are expressed in the form of equalities, such as ax+by=c.
- Non-Negative Constraints: These specify that the variables cannot take negative values, such as x≥0 and y≥0.
- For example, if we have a linear programming problem with variables x and y, the constraints might include:
- x+2y≤10 (an inequality constraint)
- 3x+y=15 (an equality constraint)
- x≥0 and y≥0 (non-negative constraints)
- In summary, constraints are essential components of linear programming problems that define the limitations on the variables. They help in determining the feasible solutions that satisfy all the given conditions.
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise - 12.1
10 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise 12.2
11 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 (C ) (True/False Questions)
5 Videos
- INVERSE - TRIGONOMETRIC FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)
11 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
Similar Questions
Knowledge Check
Observe the following reaction and answer the following questions :
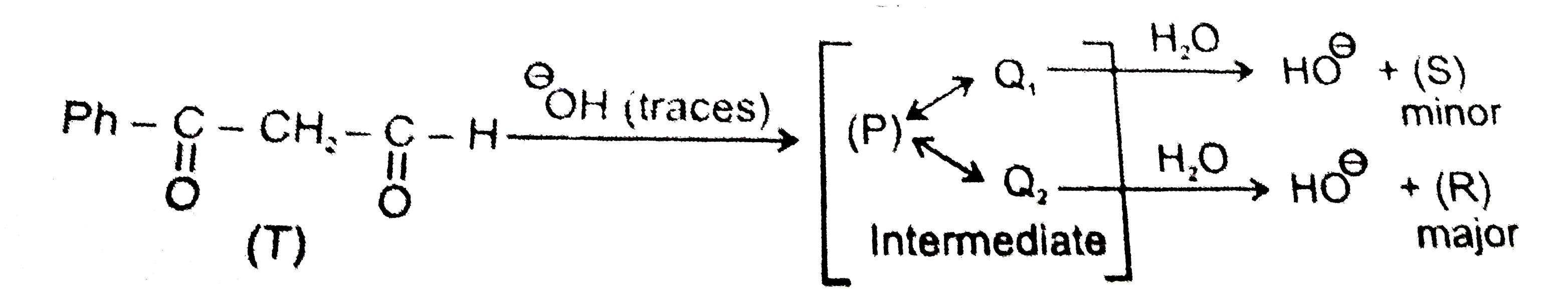
The structure of Q1 is :APh−C∣OӨ=CH−C∣∣O−HBPh−C∣OӨ=C=C∣OӨ−HCPh−C∣∣O−CH=C∣OӨ−HDPh−−∣∣OӨCH−C∣∣O−H
Answer the following questions :
What is a polymer?
View SolutionFollowing frequency distribution gives the weights of 38 students of a class :
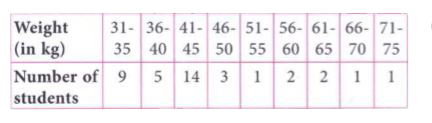
Based on the above information, answer the following questions.
Define an event whose probability is 1.
View SolutionAnswer the following questions.
Match the following:

View SolutionAnswer the following questions.
a. What are antibioties?
View SolutionAnswer the following questions briefly:
Define green revolution.
View SolutionWrite answers for the following questions
Define between mitosis and meiosis.
View Solution
Answer the following questions based on the given figure.
Define the terms mentioned in
View Solution
