(Apollonius theorem): If D is the midpoint of the side BC of a triangle ABC, then show by vector method that
∣∣∣−−→AB∣∣∣2+∣∣∣−−→AC∣∣∣2=2(∣∣∣−−→AD∣∣∣2+∣∣∣−−→BD∣∣∣2). Solution in Tamil
Step by step video & image solution for (Apollonius theorem): If D is the midpoint of the side BC of a triangle ABC, then show by vector method that |vec(AB)|^(2) + |vec(AC)|^(2) = 2(|vec(AD)|^(2)+ |vec(BD)|^(2)). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF VECTOR ALGEBRABOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF VECTOR ALGEBRAEXERCISE - SOLUTION TO EXERCISE 6.1
14 Videos
- APPLICATIONS OF VECTOR ALGEBRABOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF VECTOR ALGEBRAEXERCISE - SOLUTION TO EXERCISE 6.2
10 Videos
- APPLICATIONS OF MATRICES AND DETERMINANTS BOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE - PROBLEMS FOR PRACTICE (II. Answer the following)
15 Videos
- COMPLEX NUMBERSBOOK - PREMIERS PUBLISHERSCHAPTER - COMPLEX NUMBERSEXERCISE - Problem for practice
45 Videos
Similar Questions
Prove by vertor metord thtat if a line is drawn frome the centre of a circle of a circle to the midpoint of a chord then the line is perpendicular to the chord
View SolutionIf →a=ˆi−2ˆj+3ˆk,→b=2ˆi+ˆj−2ˆk,→c=3ˆi+2ˆj+ˆk, find →a⋅(→b×→c).
View SolutionIf A=⎡⎢⎣121112221⎤⎥⎦ verify A(adjA)=(adjA)A=|A|I3.
View SolutionIf 1−i1+i is a root of the equation
ax2+bx+1=0.
Where a, b are real than (a,b) is :
View SolutionIf DandE are the mid-points of sides ABandAC of a triangle ABC respectively, show that →BE+→DC=32→BC.
View SolutionIf D is the mid-point of the side BC of a triangle ABC, prove that →AB+→AC=2→AD.
View SolutionIf D is the mid point of side BC of a triangle ABC such that →AB+→AC=λ →AD, write the value of λ.
View SolutionIf D and E are the mid-points of sides AB and (AC of a triangle ABC respectively,show that )/(BE)+vec DC=(3)/(2)vec BC
View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
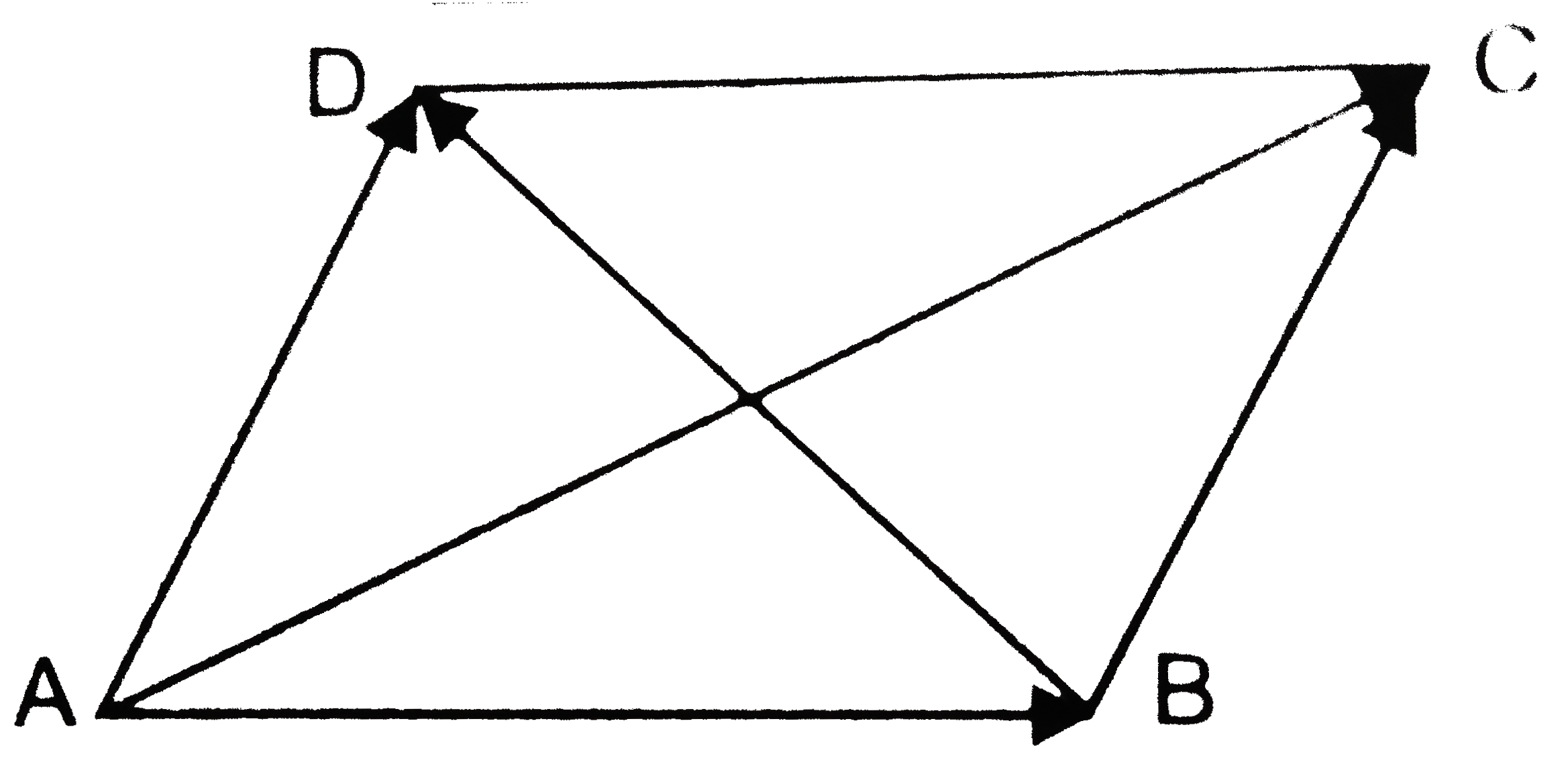 .
.
View SolutionABC एक त्रिभुज है। भुजा BC का मध्य बिंदु Dहै। सिद्ध कीजिए कि −−→AB+−−→AC=2−−→AD.
View Solutionयदि त्रिभुज ABC की भुजाओं, BC, CA व AB के मध्य बिन्दु क्रमशः D, E व F हो तो सदिश विधि से सिद्ध कीजिये कि
−−→AD+−−→BE+−−→CF=→0
View SolutionABC एक त्रिभुज हैं और D,E,F क्रमश: BC, CA, AB के मध्यबिंदु हैं| सदिश −−→BC,−−→AD,−−→BE और −−→CF को −−→AB और −−→AC के रूप में व्यक्त करें|
View SolutionIf D and E, are the midpoints of the sides AB and AC of a triangle ABC, prove that −−→BE+−−→DC=32−−→BC.
View SolutionIf D is the midpoint of the side BC of a triangle ABC, prove that vec(AB)+vec(AC)=2vec(AD)
View SolutionIf D is the midpoint of the side BC of Δ ABC then →AB+→AC=
View Solution
