Arc of a Circle
Step by step video & image solution for Arc of a Circle by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
A wire A , bent in the shape of an arc of a circle , carrying current of 2 and having radius 2 cm and another wire B, also bent in the shape of arc of a circle , carrying a current of 3 A and having radius of 4 cm , are placed as shown in the figure . The ratio of the magnetic fields due to the wires A and B at the common centre O is :
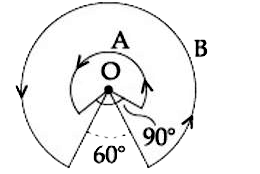 A4:6B6:4C6:5D2:5
A4:6B6:4C6:5D2:5 - Question 2 - Select One
A wire of length 'L' is bent in to an arc of a circle and found to subtentd and angle of 'θ' radians at the centre.If a current of 'I' is passed through it, the magnetic induction at the center of the circle is
Aμ0iθ22πLBμ0iθ24πLCμ0iθ4πLDμ0iθ2πL - Question 3 - Select One
A wire of length 10cm is bent into an arc of a circle such that it subtends an angle of 1 radian at the centre. If a current of 1A is passed through the wire, the magnetic induction at the centre of the circle will be
A2×10−4 teslaB1×10−6 teslaC1×10−4 teslaD2×10−6 tesla
If the length of an arc of a circle of radius a is equal to that of an arc of a circle of radius 2a, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
View SolutionTheorem:-1If two arcs of a circle are congruent ; the corresponding chord are equal and Equal chords of a circle substends equal angles at the centre.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionFigure. Shows a small loop carrying a current I. The curved portion is an arc of a circle of radius R and the straight portion is a chord to the same circle subtending an angle θ. The magnetic induction at centor O is
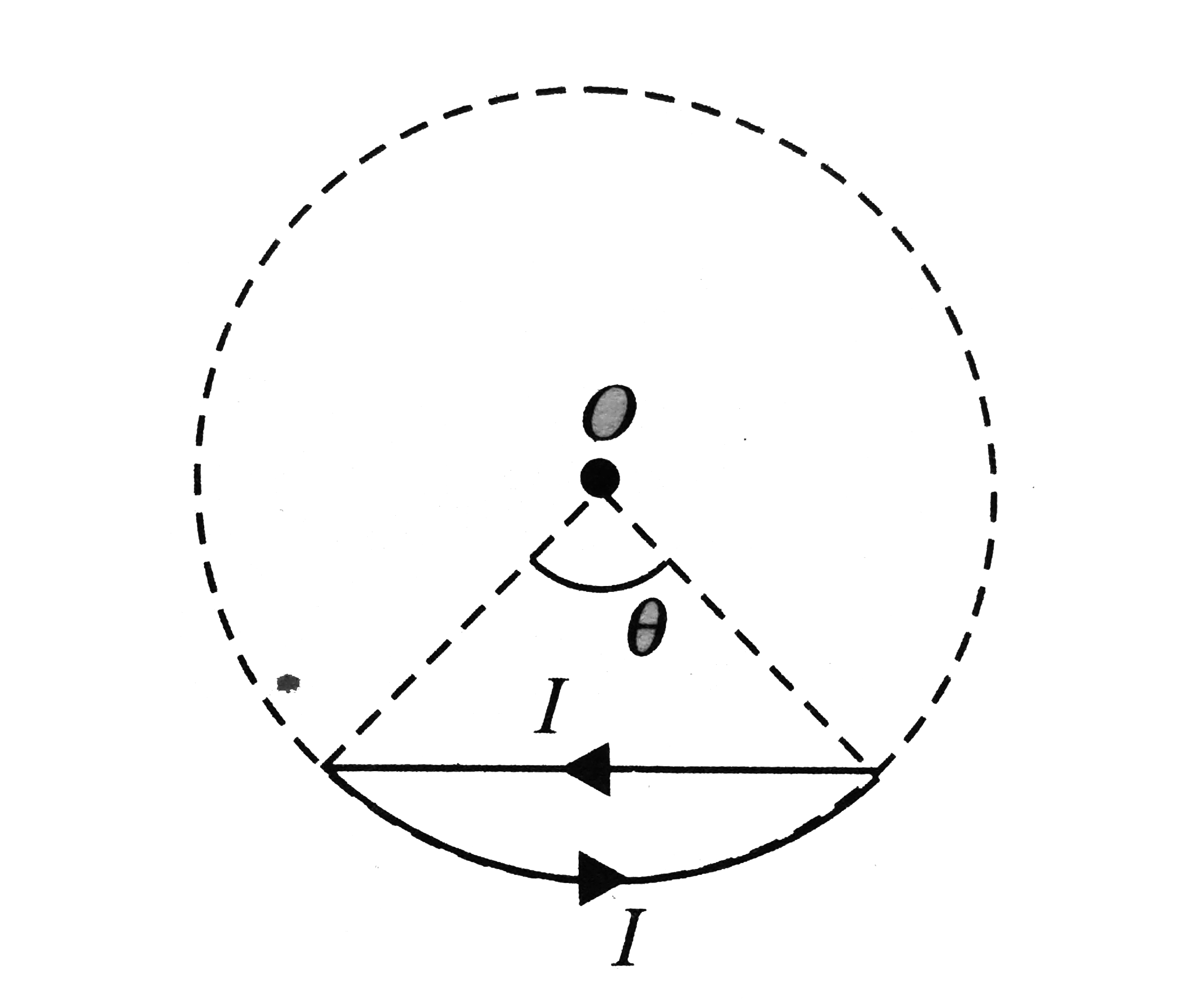 View Solution
View Solution

