Area bounded by the curves 4y=∣∣x2−4∣∣andy+|x|=7, is equal to :
A
32
B
16
C
24
D
None of these
Video Solution
Text Solution
The correct Answer is:A
4y=∣∣4−x2∣∣
⇒{4y=4−x2:−2≤x≤24y=x2−4:x<−2 or x>2
y=7−|x|
⇒ y={7+x:x<07−x:x≥0
Solving, 4y=x2−4 and y=7−x, we get x = 3.
The curves are symmetrical about Y-axis.
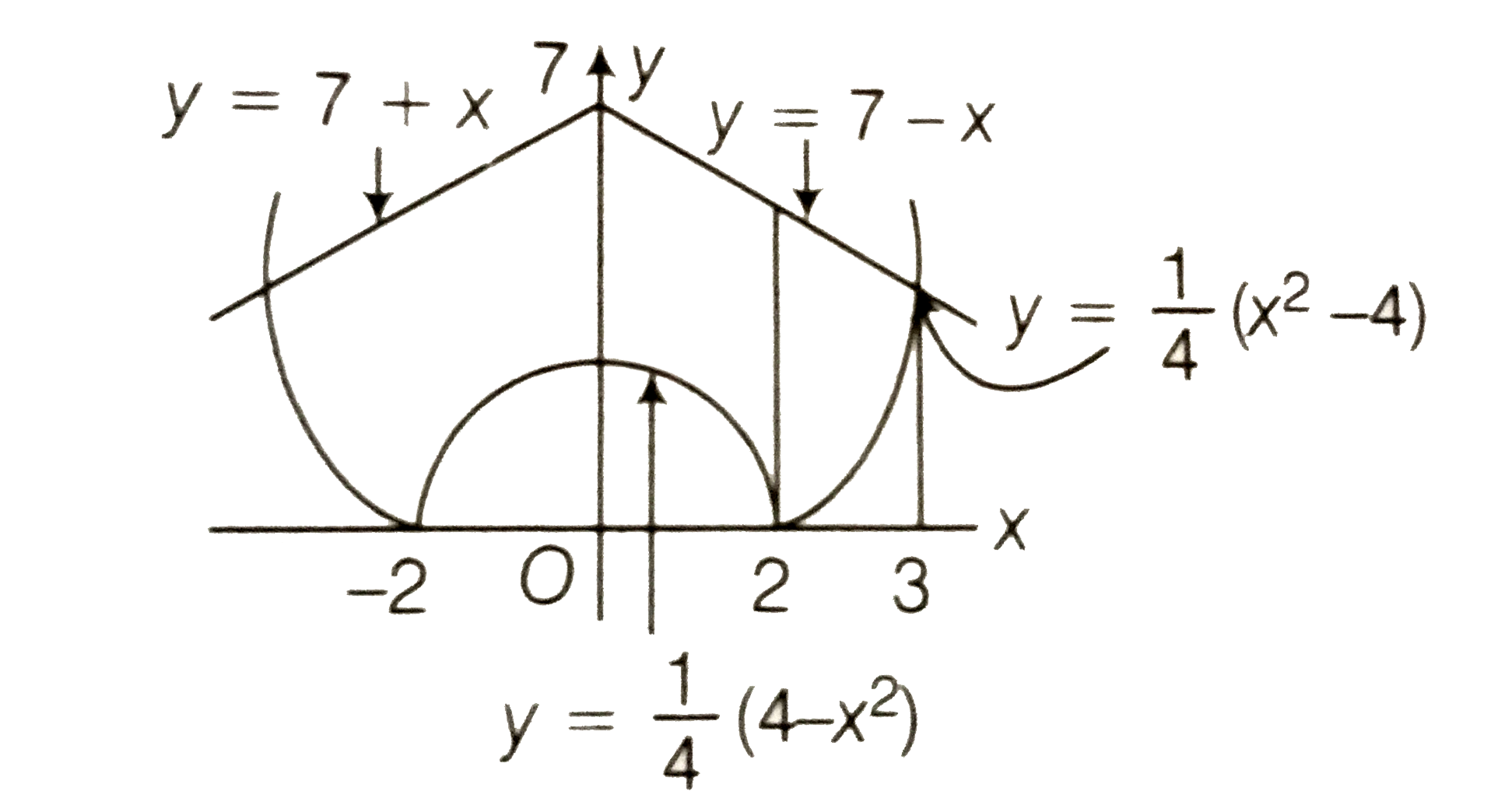
Therefore, required area
=2{∫20(7−x−14(4−x2))dx+∫32[7−x−14(x2−4)]}dx
= 32 sq units
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Area bounded by the curves y=|x|andy=4−|x| is
A4 sq unitB16 sq unitC2 sq unitD8 sq unit - Question 2 - Select One
The area of the region bounded by the curve y=x2 and y =|x| is equal to
A53 sq. unitsB13 sq. unitsC53 sq. unitsD16 sq. unit - Question 3 - Select One
The area bounded by the curves y=x2andy=2−x2 is
A83 sq unitsB3/8 sq unitsC3/2 sq unitsDNone of these
Area bounded by the curve y≥|x−2|andy≤4−|x−3|
View SolutionArea bounded by the curves y=x2−1,x+y=3 is
View SolutionThe area bounded by the curves y=2−|2−x| and |x|y=3 is
View SolutionThe area bounded by the curves y2=x3and|y|=2x is
View SolutionArea bounded by the curves y = x ,y =tanxandx=π4 is
View Solution

