Area included between curves y=x2−3x+2andy=−x2+3x−2 is
A
16 sq unit
B
12 sq unit
C
1 sq unit
D
13 sq unit
Video Solution
Text Solution
The correct Answer is:D
Intersection points of the curves are (1, 0) and (2, 0).
Therefore, required area =2∫21(−x2+3x−2)dx
=2[−x33+3x22−2x]21
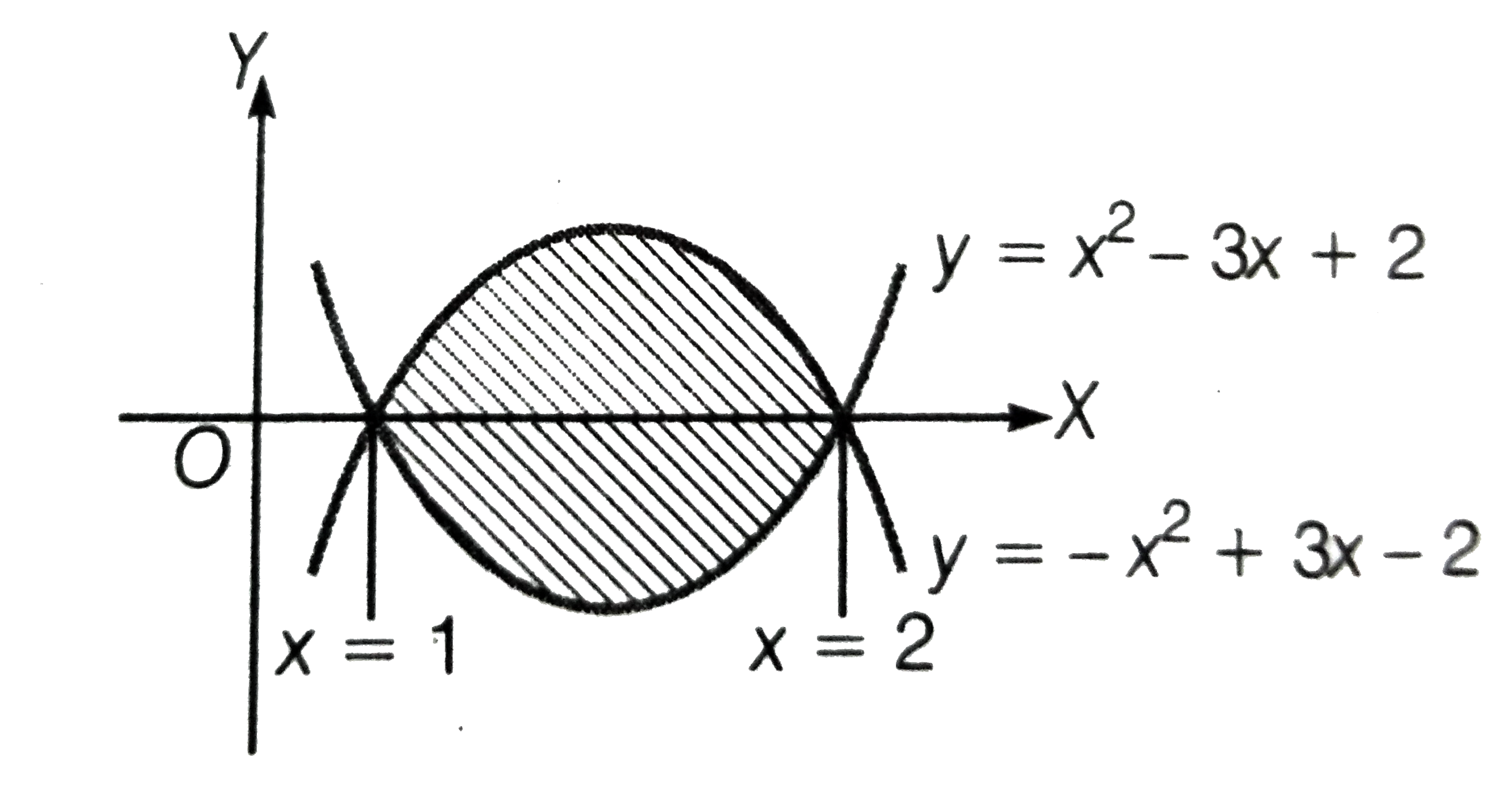
=2[−83+4−76]=13 sq unit
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 2
34 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
Area lying between the curves y2=2x and y=x is
A13 sq. unitsB34 sq. unitsC23 sq. unitsD14 sq. unitsthe area included between the curve xy2=a2(a−x) and y -axis is -
Aπa22B2πa2Cπa2DNone of theseThe area between the curves y=x2+3 and y=−x2−1 on [-2, 2] is
A803B293C21D473
the area between the curves y=x2 and y=4x is
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View Solutionfind the area enclosed between the curves y=x2−5x and y=4−2x
View SolutionArea bounded between the curves y=√4−x2 and y2=3|x| in square units is
View SolutionThe area enclosed between the curves y2=xandy=|x| is :
View Solution
