Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is
(A) $π$ (B) $\frac{π}{2}$ (C) $\frac{π}{3}$ (D) $\frac{π}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

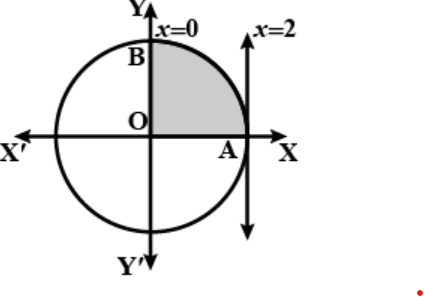
The area bounded by the circle and the lines, $x = 0$ and $x = 2$ , in the first quadrant is represented as shaded region in the plot.
Area of $△ O A B = \int_{0}^{2} y d x$
= $\int_{0}^{2} \sqrt{4 - x^{2}} d x$
$= {[\frac{x}{2} \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} (\frac{x}{2})]}_{0}^{2}$
$= 2 (\frac{π}{2})$ = $π$ sq. units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Similar Questions

Knowledge Check

Question 1 - Select One
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ the line $x = \sqrt{3} y$ and x-axis , is
A $π$
B $π / 2$
C $π / 3$
DNone of these
Question 2 - Select One
The area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the line $x = \sqrt{3} y$ is :
A $\frac{π}{3}$
B $\frac{π}{2}$
C $π$
D $\frac{π}{5}$
Question 3 - Select One
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ the line $x = \sqrt{3} y$ and x-axis , is
A $π$
B $π / 2$
C $π / 3$
D $π / 4$

Recommended Questions

Home
Ask Doubt
Profile