Question

Area of an equilateral triangle

Explanation

Area of An Equilateral Triangle

An equilateral triangle has three sides of the equal length.

They are the main normal polygon with three sides, and show up in an assortment of contexts, in both basic geometry and other advanced topics, for example, complex number geometry and geometric inequalities.

Identification of Equilateral Triangle

The simplest approach to identify an equilateral triangle is by looking along the length of the three sides. On the off chance that the three side lengths are equivalent, the structure of the triangle is resolved (an outcome of SSS congruency). Be that as it may, this is not constantly conceivable.

Another valuable paradigm is that the three points of an equilateral triangle are equivalent too, and are in this way each angle is 60∘. Since the angles opposite to equal sides are themselves equivalent, this implies finding two equivalent sides, and any 60∘ angle is adequate to consider the triangle an equilateral triangle, as is finding two equivalent angles of 60∘.

Prominently, the equilateral triangle is the one of a kind polygon for which the information on just one side length permits one to decide the full structure of the polygon. For instance, there are endlessly numerous quadrilaterals with equivalent side lengths (rhombus), so you have to know at any rate one more property to decide its full structure.

 In this context, the equilateral triangle is in accordance with the sphere and the circle whose full structures are dictated by providing just the radius.

Formula for Area of Equilateral Triangle

Let us consider an equilateral triangle with each side of  “a” units. Make a perpendicular bisector to the base of height "h".

By drawing perpendicular from A, we obtain two congruent right triangles ABD and ADC.

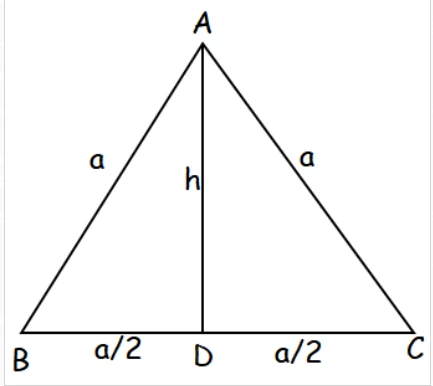
Area of ∆ ABC = Area of ∆ ADC + Area of ∆ ABD

Since ∆ ABD and ∆ ADC are congruent, areas will be equal.

Area of ∆  ABC  =  Area of ∆ ABD + Area of ∆  ADC

Area of ∆  ABC  =  2  (Area of ∆  ABD)

=  2 x (1/2) x Base x Height

Hence, Area of ∆  ABC  =  Base x Height  ---(eq. 1)

In ∆  ABD,

Base (BD)  =  a/2 and height (AD)  =  h

Using Pythagorean theorem,

a²  =  h² + (a/2)²

h²  =  a² - (a²/4)

h²  =  (3 a²/4)

h  =  √(3 a²/4)

Therefore, h  =  (a√3/2)

By putting the values of base and height in ( eq. 1), we obtain

Area of ∆  ABC  =  (a/2) x (a√3/2)  =  (1/4)a²√3

Area of ∆  ABC  =  √3a²/4

Solved Problems on Equilateral Traingle

Ques 1: Find the length of the perpendicular of an equilateral triangle of side 3√3 cm.

Soln :

length of each side of an equilateral triangle (a)  =  3√3

We know, Area of equilateral triangle  =  (√3/4) x a²

  =  (√3/4) x (3√3)²

=  (√3/4) x (27)

Area of equilateral triangle  =  27√3 / 4   --- (1)

To find the length of perpendicular,  using base x height formula for equilateral triangle

=   base x height

  =  (3√3/2) x h    ------(2)

(1)  =  (2)

(3√3/2) x h  =  27√3/4

h  =  (27√3/4) x (2/3√3)

h  =  9/2

h  =  4.5

Hence, the required perpendicular height is 4.5 cm

Ques 2: Find the area of the equilateral triangle having the length of the side of 10 cm.

Soln :

Area of equilateral triangle  =  (√3/4) a²

Here a = 10 cm

  =  (√3/4) x (10)²

  =  (√3/4) x (10) x (10)

  =  (√3) x (5) x (5)

  =  25 √3 cm²