Assertion (A) : Ltx→0|x|x=1
Reason (R) : Limit of a function doesn't exist if left and right limits exists and are not equal the correct answer is Solution in Telugu
Both A and R are true and R is the correct explanation of A
Both A and R are true and R is not the correct explanation of A
A is true but R is false
A is false but R is true
The correct Answer is:D
Step by step video, text & image solution for Assertion (A) : Lt_(x to 0)(|x|)/(x)=1 Reason (R) : Limit of a function doesn't exist if left and right limits exists and are not equal the correct answer is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITS AND CONTINUITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - SET-3Match The Following
2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
5 Videos
- LINEAR PROGRAMMING [APPENDIX-2]BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LINEAR PROGRAMMING [APPENDIX-2]EXERCISE - Exercise -1
33 Videos
Similar Questions
Match the following
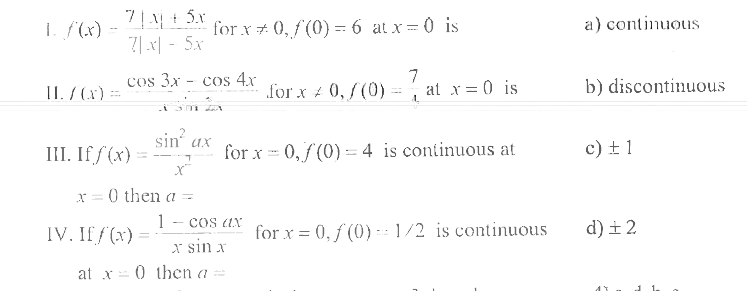
View SolutionA : The maximum value of f(x)=Sin−1x+Cos−1x−Tan−1x is 3π/4
R : Sin−1x+Cos−1x=π/2∀x∈R
View SolutionIf 2x+y≥10,x+2y≥10, then the lesat value of F=x+y is
View SolutionIf f(x)=(1)/(1+e^(-(1)/(x))),x!=0 and 0,x=0 then at x=0 (A) right hand limit of f(x) exists but not left-hand limit (B) limit of f(x) exists but not but not right-hand limit (C) both limits exists but are not equal (D) both limits exist and are equal
View Solutioncondition of existence of limit evaluation of right hand left hand limit
View SolutionIf for some real number a, Lt_(x->0 ) (sin 2x +asin x) / x^3 exists, then the limits is equal to
View Solutionफलन f(x)=12+xकीx=2 पर दक्षिण पक्ष ( Right hand limit) तथा वाम पक्ष सीमा ( Left hand limit ) ज्ञात कीजिए ।
View SolutionDo the limit of the function sin(x−[x])x−[x] exist as x→0 ? State the resons for your answer.
View SolutionDo the limits of following functions exists as x→0? State reason for your answer.
sin|x|x
View SolutionDo the limits of following functions exists as x→0? State reason for your answer.
sinx|x|
View SolutionDo the limits of following functions exists as x→0? State reason for your answer.
x⌊x⌋sin|x|
View SolutionDo the limits of following functions exists as x→0? State reason for your answer.
sin(x−⌊x⌋)x−⌊x⌋
View SolutionEvaluate the limits, if exist(lim)x→0esinx−1x
View SolutionEvaluate the limits, if exist(lim)x→0e4x−1x
View SolutionProve that as x→1, the functions f(x)={x+10≤x<13x+21<x≤3 has a limit to the left equal to 2 and a limit to the right equal to 5.
View Solution
