Assertion (A) : PA and PB are triangles to a circle with centre O such that ∠AOB=110∘, then ∠APB=90∘
Reason (R ) : The length of two tangents drawn from an external point are equal .
Both A and R are true and R is the correct explanation for A.
Both A and R are true and R is not correct explanation for A.
A is true but R is false.
A is false but R is true.
The correct Answer is:D
To solve the problem, we need to analyze the assertion and the reason given:
1. Understanding the Assertion:
- The assertion states that if PA and PB are tangents to a circle with center O, and the angle AOB is 110°, then the angle APB is 90°.
2. Drawing the Diagram:
- Draw a circle with center O. Mark point P outside the circle. Draw tangents PA and PB from point P to the circle, touching the circle at points A and B respectively.
3. Identifying Angles:
- According to the properties of tangents, the angle between the tangent and the radius at the point of contact is 90°. Thus, ∠OAP = 90° and ∠OBP = 90°.
4. Using the Angle Sum Property:
- In quadrilateral OAPB, the sum of the angles is 360°. We know:
- ∠OAP = 90°
- ∠OBP = 90°
- ∠AOB = 110°
- Let ∠APB = x. Therefore, we can write the equation:
x+90°+110°+90°=360°
5. Simplifying the Equation:
- Combine the known angles:
x+290°=360°
- Now, isolate x:
x=360°−290°=70°
6. Conclusion about Assertion:
- We found that ∠APB = 70°, not 90°. Hence, the assertion is false.
7. Understanding the Reason:
- The reason states that the lengths of two tangents drawn from an external point are equal. This is a true statement based on the properties of tangents.
8. Final Evaluation:
- Since the assertion is false and the reason is true, we conclude that the assertion (A) is false and the reason (R) is true.
Final Answer:
- Assertion (A) is false.
- Reason (R) is true.
- The assertion states that if PA and PB are tangents to a circle with center O, and the angle AOB is 110°, then the angle APB is 90°.
- Draw a circle with center O. Mark point P outside the circle. Draw tangents PA and PB from point P to the circle, touching the circle at points A and B respectively.
- According to the properties of tangents, the angle between the tangent and the radius at the point of contact is 90°. Thus, ∠OAP = 90° and ∠OBP = 90°.
- In quadrilateral OAPB, the sum of the angles is 360°. We know:
- ∠OAP = 90°
- ∠OBP = 90°
- ∠AOB = 110°
- Let ∠APB = x. Therefore, we can write the equation:
x+90°+110°+90°=360°
- Combine the known angles:
x+290°=360°
- Now, isolate x:
x=360°−290°=70°
- We found that ∠APB = 70°, not 90°. Hence, the assertion is false.
- The reason states that the lengths of two tangents drawn from an external point are equal. This is a true statement based on the properties of tangents.
- Since the assertion is false and the reason is true, we conclude that the assertion (A) is false and the reason (R) is true.
- Assertion (A) is false.
- Reason (R) is true.
Topper's Solved these Questions
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - CASE -BASED MCQs
15 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTIONS
47 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT
5 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Assertion and Reasoning Based Questions
2 Videos
Similar Questions
Knowledge Check
If PA and PB are tangents to the circle with centre O such that ∠APB=50∘ then ∠OAB is equal to
A50∘B30∘C40∘D25∘In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
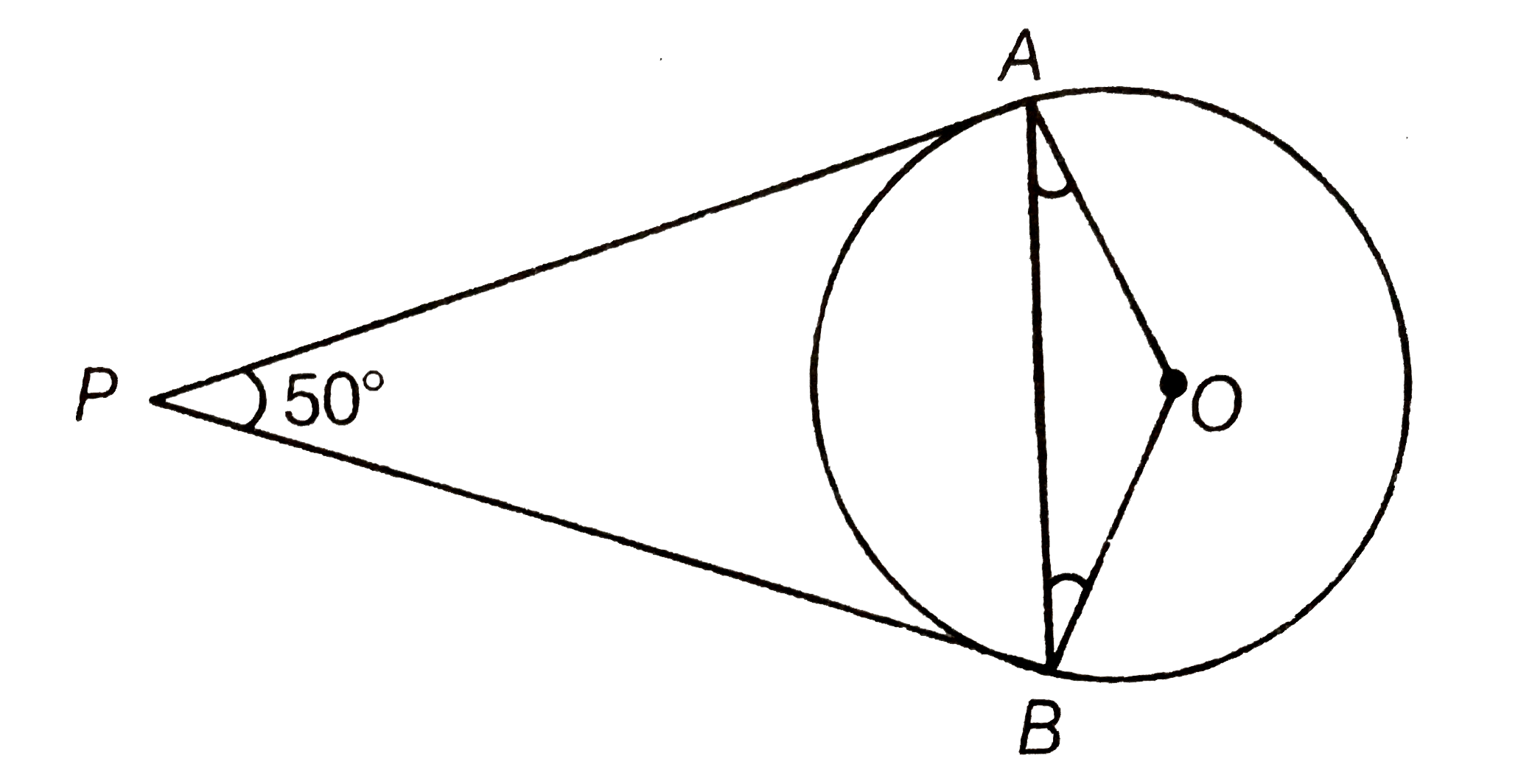 A25∘B30∘C40∘D50∘
A25∘B30∘C40∘D50∘If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
A40∘B50∘C60∘D70∘
Prove that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionCompare the length of the tangents drawn from the external point to circle.
View Solution
The length of tangents drawn from the external point to a circle are ........... .
View SolutionIn the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
View Solution
