At a child's lemonade stand, p pitchers of lemonade are made by adding m packets of lemonade mix to cold water. If m=2p+4, how many more packets of lemonde mix are needed to make each additional pitcher of lemonade ?
0
1
2
4
The correct Answer is:C
To solve the problem step by step, we need to determine how many additional packets of lemonade mix are needed for each additional pitcher of lemonade.
Step 1: Understand the relationship between pitchers and packets
We are given that the number of packets of lemonade mix m needed for p pitchers is given by the equation:
m=2p+4
Step 2: Calculate the packets needed for p pitchers
Using the formula, for p pitchers, the number of packets needed is:
m=2p+4
Step 3: Calculate the packets needed for p+1 pitchers
Now, we need to find out how many packets are needed for p+1 pitchers. We substitute p+1 into the formula:
m=2(p+1)+4
This simplifies to:
m=2p+2+4=2p+6
Step 4: Determine the difference in packets between p+1 and p
Now we need to find out how many more packets are needed when going from p pitchers to p+1 pitchers. We subtract the number of packets needed for p pitchers from the number needed for p+1 pitchers:
(2p+6)−(2p+4)
Step 5: Simplify the expression
Now, simplify the expression:
(2p+6)−(2p+4)=2p+6−2p−4=2
Conclusion
Thus, the number of additional packets of lemonade mix needed to make each additional pitcher of lemonade is:
2
We are given that the number of packets of lemonade mix m needed for p pitchers is given by the equation:
m=2p+4
Using the formula, for p pitchers, the number of packets needed is:
m=2p+4
Now, we need to find out how many packets are needed for p+1 pitchers. We substitute p+1 into the formula:
m=2(p+1)+4
This simplifies to:
m=2p+2+4=2p+6
Now we need to find out how many more packets are needed when going from p pitchers to p+1 pitchers. We subtract the number of packets needed for p pitchers from the number needed for p+1 pitchers:
(2p+6)−(2p+4)
Now, simplify the expression:
(2p+6)−(2p+4)=2p+6−2p−4=2
Thus, the number of additional packets of lemonade mix needed to make each additional pitcher of lemonade is:
2
Topper's Solved these Questions
Similar Questions
At a restaurant , n cups of tea are made by adding t tea bags to hot water. IF t=n+2. how many additional tea bugs are needed to make each additional cup of tea?
View SolutionAn amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μsR/g)1/2
b. Obtain a numerical value for T taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c. If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d. If instead the cylinder rate revolution is made to be somewhat smaller what happens to the magnitude and what happens to the motion of the person ?
View Solution
Knowledge Check
Aubrie, Bera, and Kea are running a lemonade and snack stand to earn money. They are sellling lemonade for $1.07 a cup and chocolate chip cookies for $0.78 each. Their customers arrive on foot or by car. During a three hour period, they had 47 customers each buying only one item and made $45.94. Aubrie, Bera, and Kea need to determine if they have enough supplies for tomorrow. Solving which of the following system of equations will let them know many cups of lemonade, x, and how many cookies , y, they sold today?
A{x+y=45.941.07x+0.78y=47B{x+y=471.07x+0.78y=45.94C{x+y=470.78x+1.07y=45.94D{x+y=47107x+78y=45.94This passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
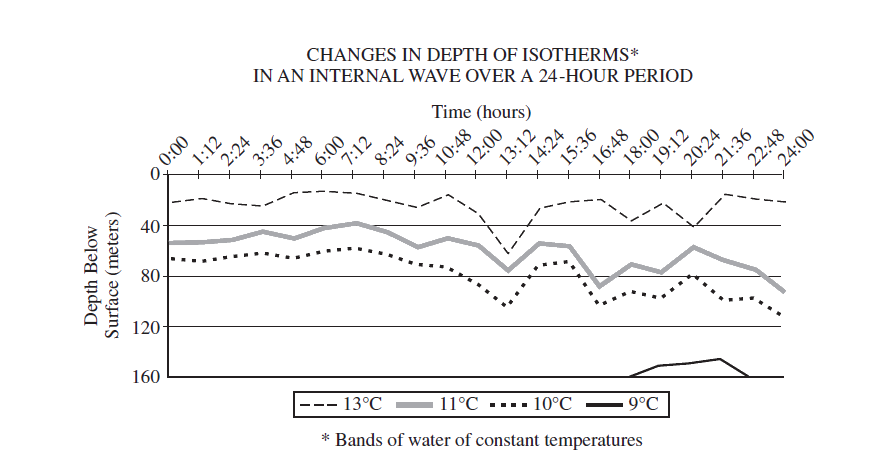
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
The first paragraph serves mainly toAexplain how a scientific device is used.Bnote a common misconception about an event.Cdescribe a natural phenomenon and address its importance.Dpresent a recent study and summarize its findings.This passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
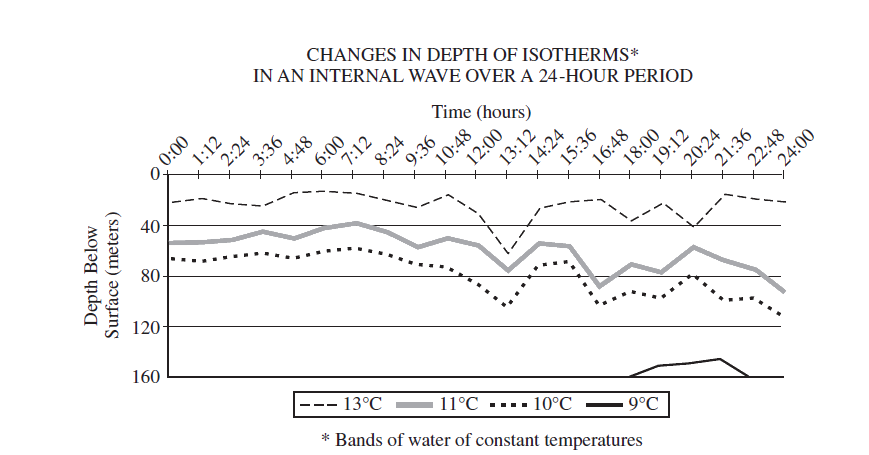
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
Which choice provides the best evidence for the answer to the previous question?ALines 1-2 (“Some . . . see”)BLines 4-6 (“they . . . equipment”)CLines 17-19 (“If . . . this”)DLines 24-26 (“Internal . . . high”)
This passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
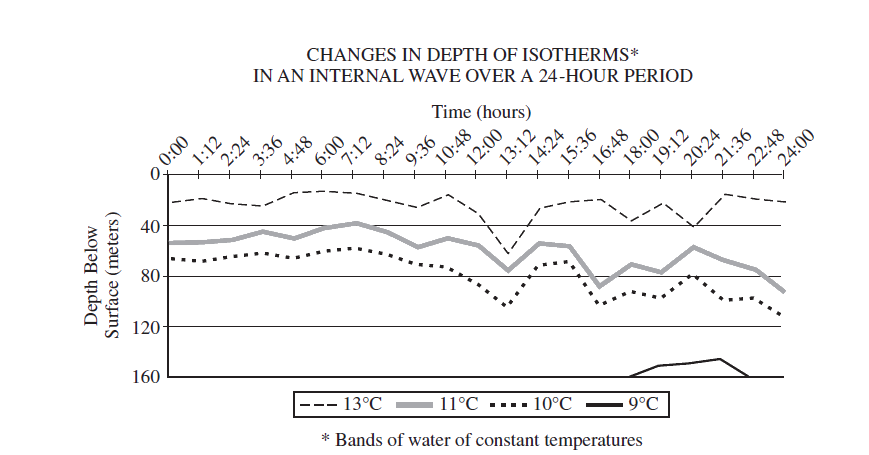
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
As used in line 65, “devise” most nearly means
View SolutionThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
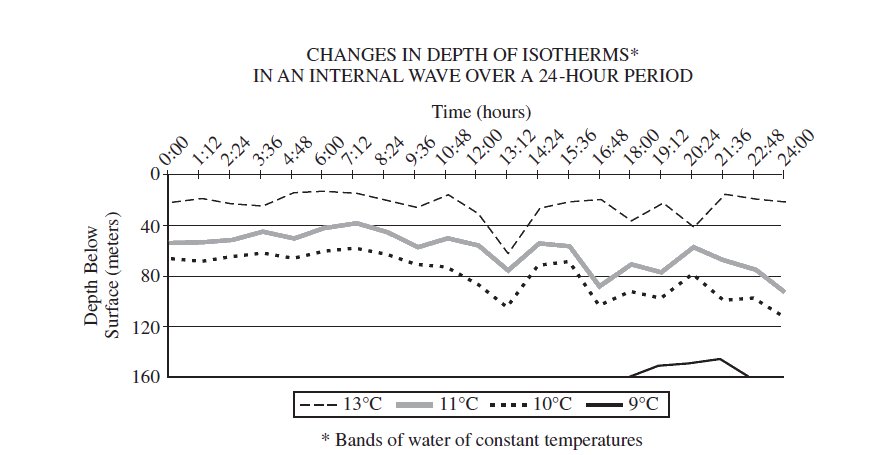
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
As used in line 19, “capture” is closest in meaning to
View SolutionThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
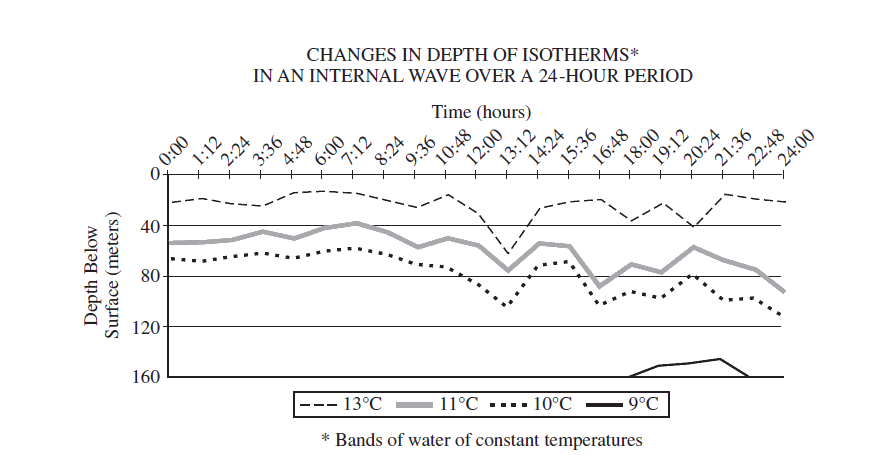
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
According to Peacock, the ability to monitor internal waves is significant primarily because
View SolutionThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
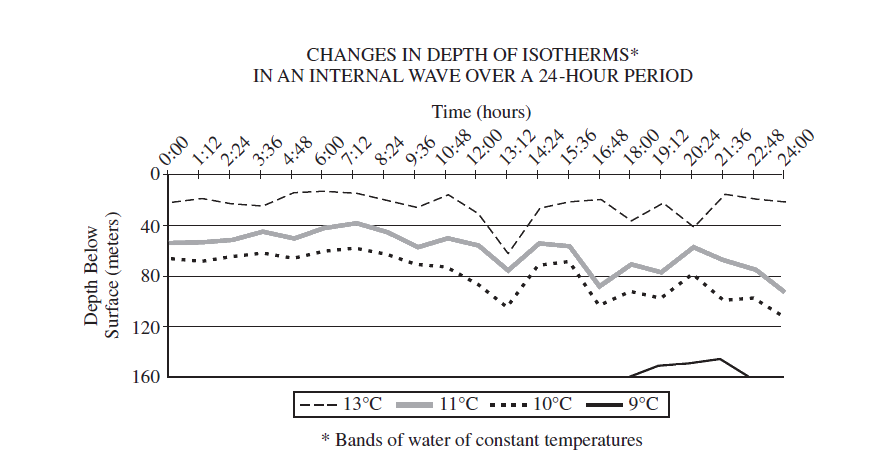
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
In the graph, which isotherm displays an increase in depth below the surface during the period 19:12 to 20:24?
View SolutionThis passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
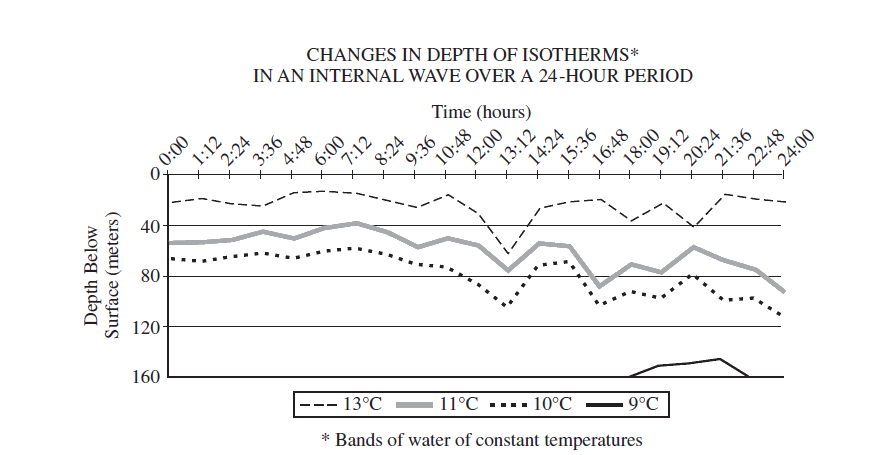
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
Which choice provides the best evidence for the answer to the previous question?
View Solution
