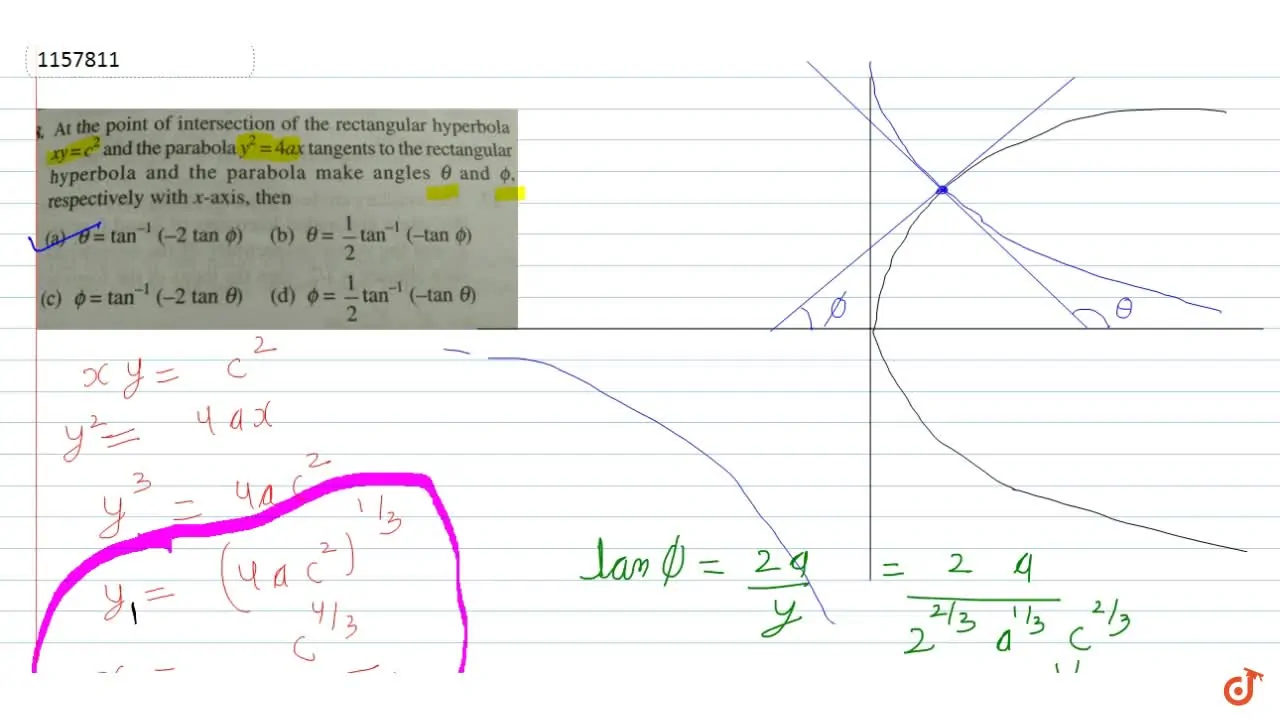
At the point of intersection of the rectangular hyperbola xy=c2 and the parabola y2=4ax tangents to the rectangular hyperbola and the parabola make angles θ and ϕ , respectively with x-axis, then
θ=tan−1(−2tanϕ)
θ=12tan−1(−tanϕ)
ϕ=tan−1(−2tanθ)
ϕ=12tan−1(−tanθ)
The correct Answer is:A
Let (x1,y1) be point of intersection
⇒y21=4ax1,x1y1=c2
y2=4axxy=c2
mT(x1,y1)=2ay1=tanϕ
MT(x1,y1)=−y1x1=tanθ
So tanθtanϕ=−y212ax1=−4ax12ax1=−2
So θ=tan−1(−2tanϕ)
Similar Questions
Show that for rectangular hyperbola xy=c2
View SolutionThe parametric form of rectangular hyperbola xy=c2
View SolutionIf lx+my+n=0 is a tangent to the rectangular hyperbola xy=c2, then
View SolutionThe parabola y2=4x cuts orthogonally the rectangular hyperbola xy=c2 then c2=
View Solution. A straight line touches the rectangular hyperbola 9x2−9y2=8 and the parabola y2=32x. An equation of the line is
View SolutionThe coordinates of a point on the rectangular hyperbola xy=c2 normal at which passes through the centre of the hyperbola are
View SolutionFind the length of that focal chord of the parabola y2=4ax, which touches the rectangular hyperbola 2xy=a2 .
View SolutionA,B,C are three points on the rectangular hyperbola xy=c2, The area of the triangle formed by the tangents at A,BandC.
View SolutionThe locus of the point of intersection of the tangents to the parabola y2=4ax which include an angle α is
View SolutionA normal to the parabola y2=4ax with slope m touches the rectangular hyperbola x2−y2=a2 if
View Solution