Attempt this question on graph paper.
Write down :
the measure of angle ABB'
The correct Answer is:45∘
To solve the question of finding the measure of angle ABB' on a graph paper, let's follow these steps:
1. Assume Points A and B:
Let's assume point A has coordinates (1, 2) and point B has coordinates (2, 3).
2. Determine Point B':
Since B' is the reflection of point B across the x-axis, we can find the coordinates of B' by changing the sign of the y-coordinate of B.
- The coordinates of B are (2, 3), so the coordinates of B' will be (2, -3).
3. Plot Points on Graph Paper:
- Plot point A at (1, 2).
- Plot point B at (2, 3).
- Plot point B' at (2, -3).
4. Draw Lines:
- Draw a line segment from A to B.
- Draw a line segment from A to B'.
- You should now have two lines: AB and AB'.
5. Identify Angle ABB':
- The angle ABB' is formed between the line segments AB and AB'.
- To find the measure of angle ABB', we can use the slopes of the lines.
6. Calculate the Slopes:
- The slope of line AB = (y2 - y1) / (x2 - x1) = (3 - 2) / (2 - 1) = 1.
- The slope of line AB' = (y2 - y1) / (x2 - x1) = (-3 - 2) / (2 - 1) = -5.
7. Find the Angle Using the Tangent Formula:
- The tangent of the angle θ between two lines with slopes m1 and m2 is given by:
tan(θ)=m1−m21+m1⋅m2
- Here, m1 = 1 and m2 = -5:
tan(θ)=1−(−5)1+(1)(−5)=61−5=6−4=−32
8. Calculate the Angle:
- To find the angle θ, we can use the arctan function:
θ=tan−1(−32)
- This will give us an angle of approximately 45 degrees.
9. Conclusion:
- Therefore, the measure of angle ABB' is 45 degrees.
Let's assume point A has coordinates (1, 2) and point B has coordinates (2, 3).
Since B' is the reflection of point B across the x-axis, we can find the coordinates of B' by changing the sign of the y-coordinate of B.
- The coordinates of B are (2, 3), so the coordinates of B' will be (2, -3).
- Plot point A at (1, 2).
- Plot point B at (2, 3).
- Plot point B' at (2, -3).
- Draw a line segment from A to B.
- Draw a line segment from A to B'.
- You should now have two lines: AB and AB'.
- The angle ABB' is formed between the line segments AB and AB'.
- To find the measure of angle ABB', we can use the slopes of the lines.
- The slope of line AB = (y2 - y1) / (x2 - x1) = (3 - 2) / (2 - 1) = 1.
- The slope of line AB' = (y2 - y1) / (x2 - x1) = (-3 - 2) / (2 - 1) = -5.
- The tangent of the angle θ between two lines with slopes m1 and m2 is given by:
tan(θ)=m1−m21+m1⋅m2
- Here, m1 = 1 and m2 = -5:
tan(θ)=1−(−5)1+(1)(−5)=61−5=6−4=−32
- To find the angle θ, we can use the arctan function:
θ=tan−1(−32)
- This will give us an angle of approximately 45 degrees.
- Therefore, the measure of angle ABB' is 45 degrees.
Similar Questions
Knowledge Check
If an angle is one-third of its supplement, then the measure of the angle is
A45∘B30∘C135∘D150∘
Attempt this question on graph paper.
Write down :
the single transformation that maps A' to A''.
View SolutionAttempt this question on graph paper.
Reflect A and B in the x-axis to A' and B' respectively. Plot these points also on the same graph paper.
View Solution
Write down the name of point A
View SolutionWrite down the IUPAC name of
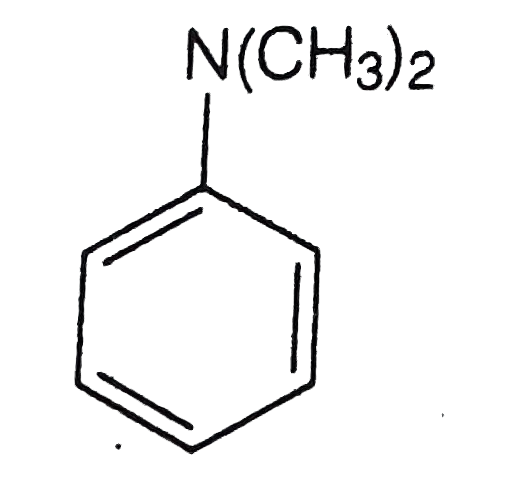
View SolutionAttempt this question on graph paper.
Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
View SolutionPlot the points A(9,6) and B(5,9) on the graph paper. These two points are the vertices of a figure ABCD which is symmetrical about x = 5 and y = 6. Complete the figure on the graph. Write down the geometrical name of the figure.
View SolutionAngles A and B are complementary and the measure of angle A is twice the measure of angle B. Find the measures of angles A and B
View Solution
