Question

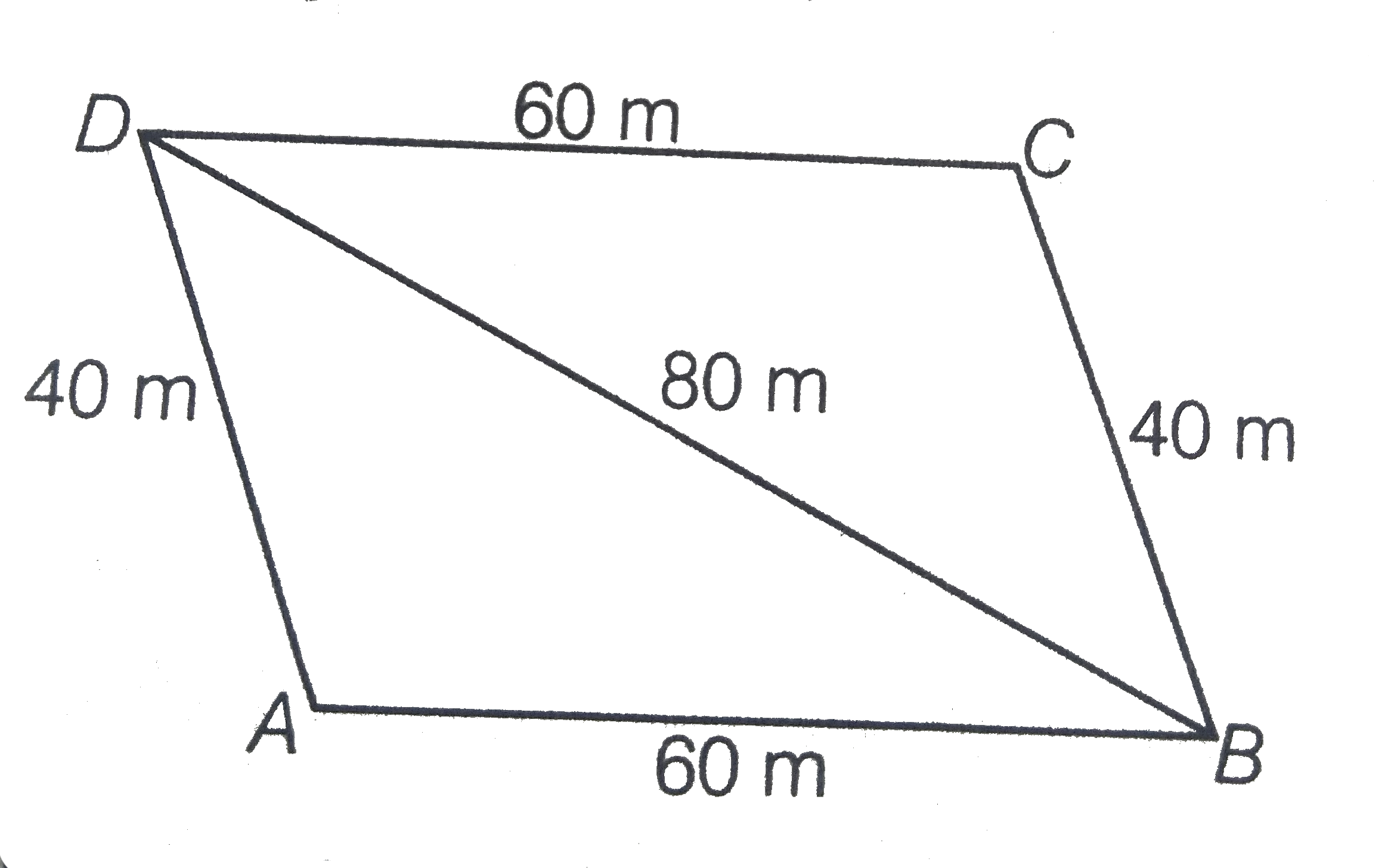
Atul is playing in a playground which is of the form of a parallelogram. He observes that the diagonals of the playground are 80 m and 60 m long. So, the playground can be the shape of ____

Options

A. Rectangle
B. Rhombus
C. Kite
D. Square

Answer

B

Explanation

To determine the shape of the playground that Atul is playing in, we need to analyze the properties of the diagonals of a parallelogram.

1. Understanding the Properties of Diagonals in Parallelograms:
- In a parallelogram, the diagonals bisect each other but are not necessarily equal in length.

2. Given Information:
- The lengths of the diagonals are 80 m and 60 m.

3. Identifying the Possible Shapes:
- The question states that the playground is in the form of a parallelogram. The common types of parallelograms are rectangles, rhombuses, and squares.
- In rectangles and squares, the diagonals are equal. Since the diagonals here are 80 m and 60 m (which are not equal), the playground cannot be a rectangle or a square.

4. Considering Rhombus and Kite:
- A rhombus is a type of parallelogram where the diagonals are not equal but they bisect each other at right angles.
- A kite is not a parallelogram, so it cannot be considered in this case.

5. Conclusion:
- Since the only remaining option that fits the description of having unequal diagonals while still being a parallelogram is a rhombus, we conclude that the shape of the playground must be a rhombus.

Final Answer:
The playground can be the shape of a rhombus.