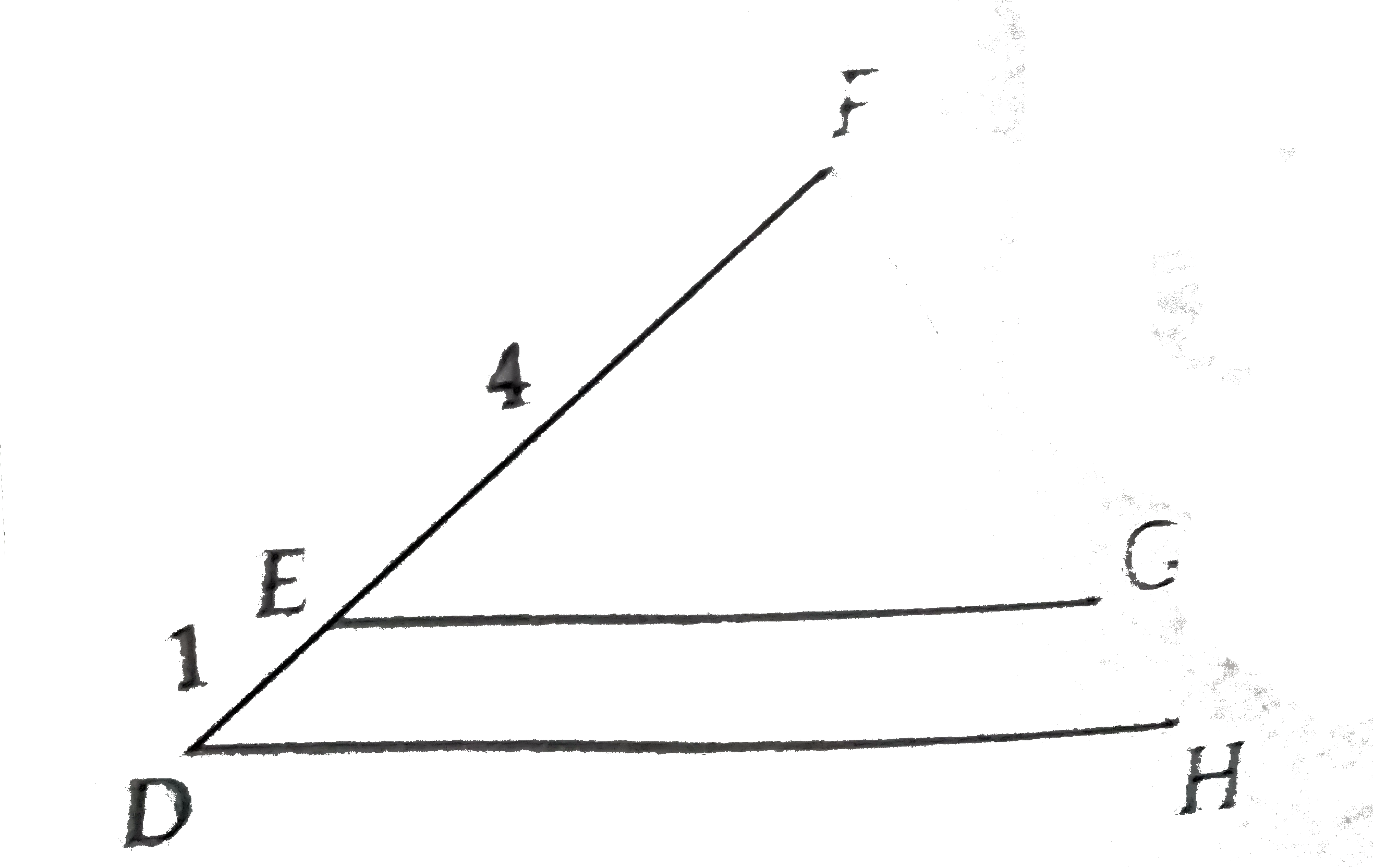
¯¯¯¯¯¯EG∣∣¯¯¯¯¯¯¯DH, and the length of segments ¯¯¯¯¯¯DE and ¯¯¯¯¯¯EF are as marked. If the area of ΔEFG is a, what is the area of ΔDFH in terms of a ?
A
4a5
B
16a25
C
16a20
D
25a16
Video Solution
Text Solution
The correct Answer is:D
The only information that's in the question and not is the figure is that ¯¯¯¯¯¯EG and ¯¯¯¯¯¯¯DH are parallel and that the area of ΔEFG is a. That ¯¯¯¯¯¯EG and ¯¯¯¯¯¯¯DH are parallel tells you that ΔEFG and ΔDEFH are similar - they have the same angles, and sides are in proportion. Because the ratio of ¯¯¯¯¯¯DF to ¯¯¯¯¯¯EF is 54, the ratio of any pair of corresponding sides will also be 54. But that's not the ratio of the areas. Remember that the ratio of the areas of similar triangles is the square of the ratio of the sides. Here the side ratio is 54, so the area ratio is 5242=2516. If the area of the small triangle is a, then the area of the large one is 25a16.
|
Topper's Solved these Questions
- PLANE GEOMETRY BOOK - KAPLANCHAPTER - PLANE GEOMETRY EXERCISE - PLANE GEOMETRY FOLLOW - UP TEST
6 Videos
- MISCELLANEOUS TOPICS BOOK - KAPLANCHAPTER - MISCELLANEOUS TOPICS EXERCISE - MISCELLANEOUS TOPICS FOLLOW - UP TEST
12 Videos
- PRACTICE TEST 1 BOOK - KAPLANCHAPTER - PRACTICE TEST 1 EXERCISE - PRACTICE TEST
50 Videos
Similar Questions
Knowledge Check

What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
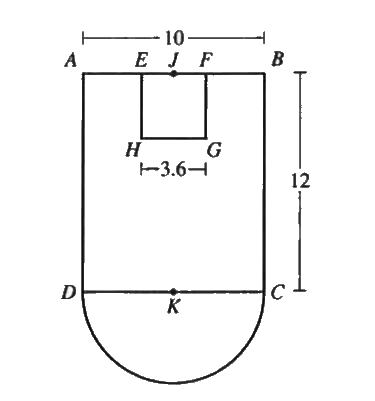
What is the length, in meters, of ¯¯¯¯¯¯JD?A13B15.6C17D√44In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
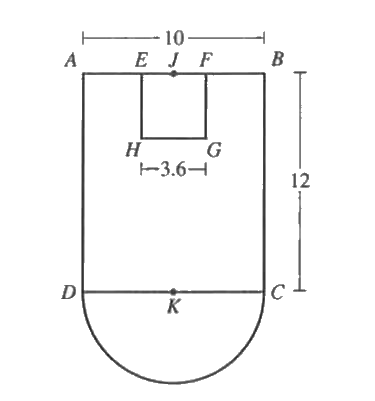
What is the length, in meters, of are ¯¯¯¯¯¯CD?A2.5πB5πC6.25πD10π
If the midpoints of segments ¯¯¯¯¯¯¯GH,¯¯¯¯¯¯JK,¯¯¯¯¯¯¯LM are connected, what is the area of the resulting triangle ?

View SolutionIn triangle DEF,DE=DF=10andEF=16. What is the area of the triangle?
View SolutionMagnetic length of a bar magnet is
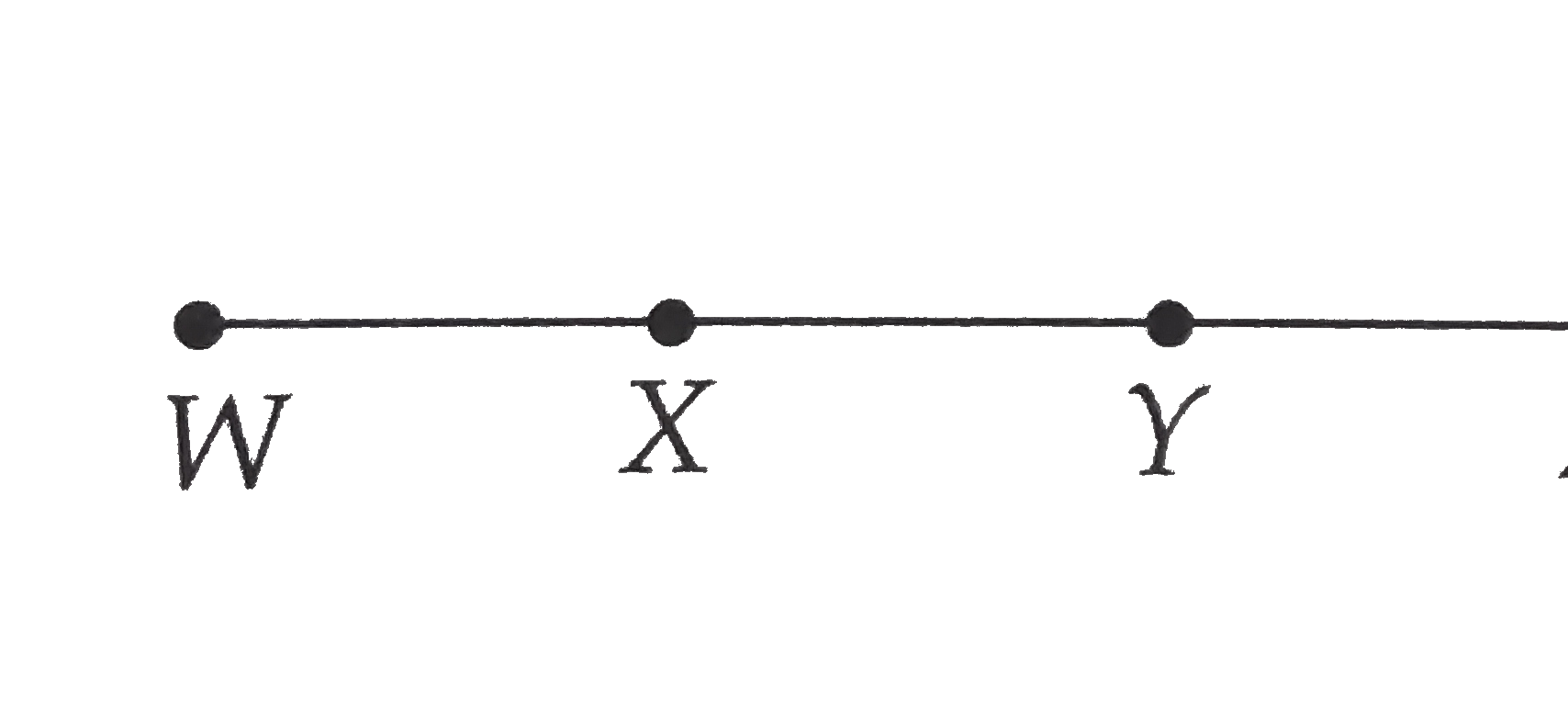
View SolutionThe length of ¯¯¯¯¯¯¯WZ is 3a+15, and the length of ¯¯¯¯¯¯¯WX is 7a+5. If Y is the midpoint of ¯¯¯¯¯¯XZ, what is the length of ¯¯¯¯¯¯¯WY ?
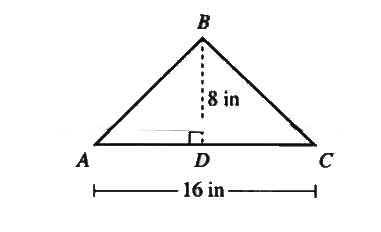
View SolutionFor △ABC shown below, base ¯¯¯¯¯¯AC has a length of 16 inches and altitude ¯¯¯¯¯¯BD has a length of 8 inches. The area of a certain square is equal to the area of △ABC. What is the length, in inches, of a side of the square?
View Solution