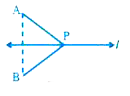
Based on Playfair's axiom, for every line I and every point P not lying on l, there exists ____ line (s) passing through P and parallel to I.
Two distinct
A unique
Three distinct
None of these
The correct Answer is:B
Step by step video, text & image solution for Based on Playfair's axiom, for every line I and every point P not lying on l, there exists ____ line (s) passing through P and parallel to I. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Everyday mathematics10videos
IMO QUESTION PAPER 2016 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Achievers section5videos
IMO QUESTION PAPER 2016 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET A EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2016 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2017 SET B
Similar Questions
Knowledge Check
- Question 1 - Select One
Every point on a number line represents.
Aa rational numberBa natural numberCan irrational numberDa unique real number
Equation of line passing through a given point and parallel to given line
View SolutionDraw a line AB. Take a point P outside it. Draw a line passing through P and perpendicular to AB.
View SolutionDraw a line AB. Take a point P on it. Draw a line passing through P and perpendicular to AB.
View SolutionEquation of plane passes through two points and parallel to a line
View Solution.If l is any given line and P is any point not lying on it, then the number of parallel lines that can be drawn through P, parallel to I would be
View Solutiona pair of lines passing through the point (3,d) and parallel to coordinate axes
View SolutionIf B is the image of the point A with respect to the line l and P is any point lying on l, then the lengths of line segments PA and PB are _______.
 View Solution
View Solution

