BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
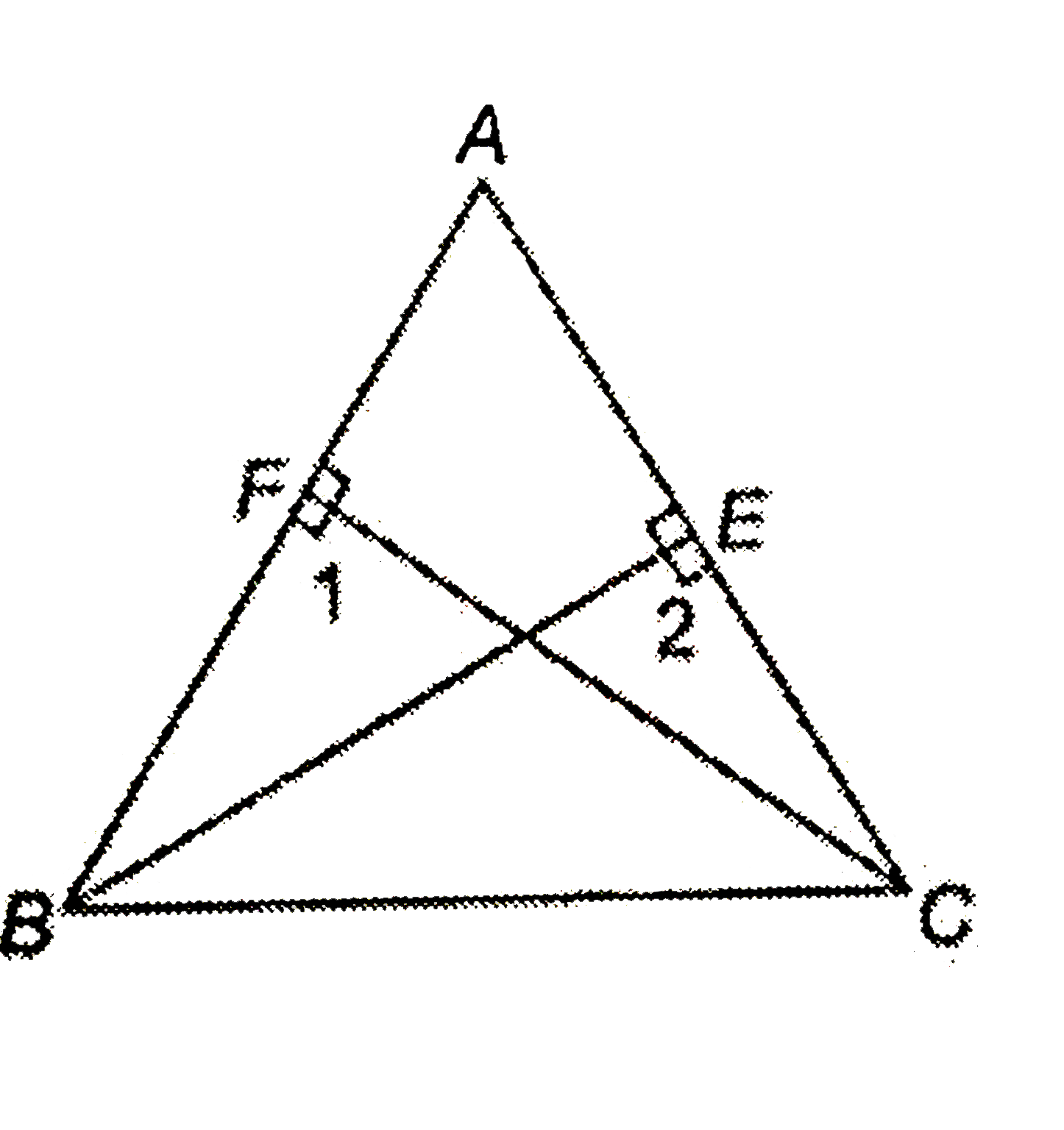
Given : ΔABC in which BE and CF are the altitudes such that BE=CF. To prove : ΔABC is an isosceles triangle i.e., AB=AC.
Proof : Since BE and CF are the altitudes
∴∠1=∠2 (each 90∘)
Now, in ΔBFC and ΔBEC,
∵⎧⎪⎨⎪⎩∠1=∠2(given)BC=BC(common)CF=BE(given)
∴ΔBFC≅ΔBEC (RIIS)
∴∠B=∠C (c.p.c.t)
⇒AC=AB (sides opposite to equal angles are equal)
∴ΔABC is an isosceles triangle. Hence Proved.
We can also prove this by taking AAS congruence rule in Δs ABE and AFC, if no particular method is asked)

Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
View SolutionIf the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
In△ABEand △ACF∠AEB=∠AFC(900each)
∠BAE=∠CAF(common angle)
∠ABE=∠ACF using angle sum property
BE=CF,△ABE≅△ACF
⇒AB=AC
Hence triangle ABC is an isosceles tangent as two sides are equal to each otherView Solution
Knowledge Check
- Question 1 - Select One
BE and CF are two altitudes of a triangle ABC. If AB=6cm,AC=5cmand CF=4cm, then the length of BE is
A4.8 cmB7.5 cmC3.33 cmD5.5 cm - Question 2 - Select One
If AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEA
In a triangle ABC, if ∠A=∠B+∠C, the prove that triangle ABC is a right triangle.
View SolutionIf in a ΔABC,c(a+b)cosB/2=b(a+c)cosC/2, prove that the triangle is isosceles.
View SolutionIn △ABC, if cosA+sinA−2cosB+sinB=0 then prove that triangle is isosceles right angled.
View SolutionIn figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
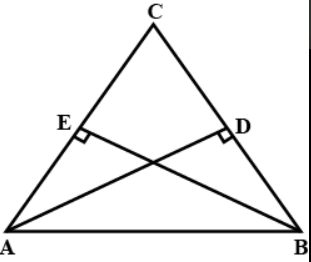 View Solution
View SolutionIn a ΔABC if (a+b)cos(B2)=b(a+c)cos(C2) then prove that the triangle ABC is isosceles.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View Solution
