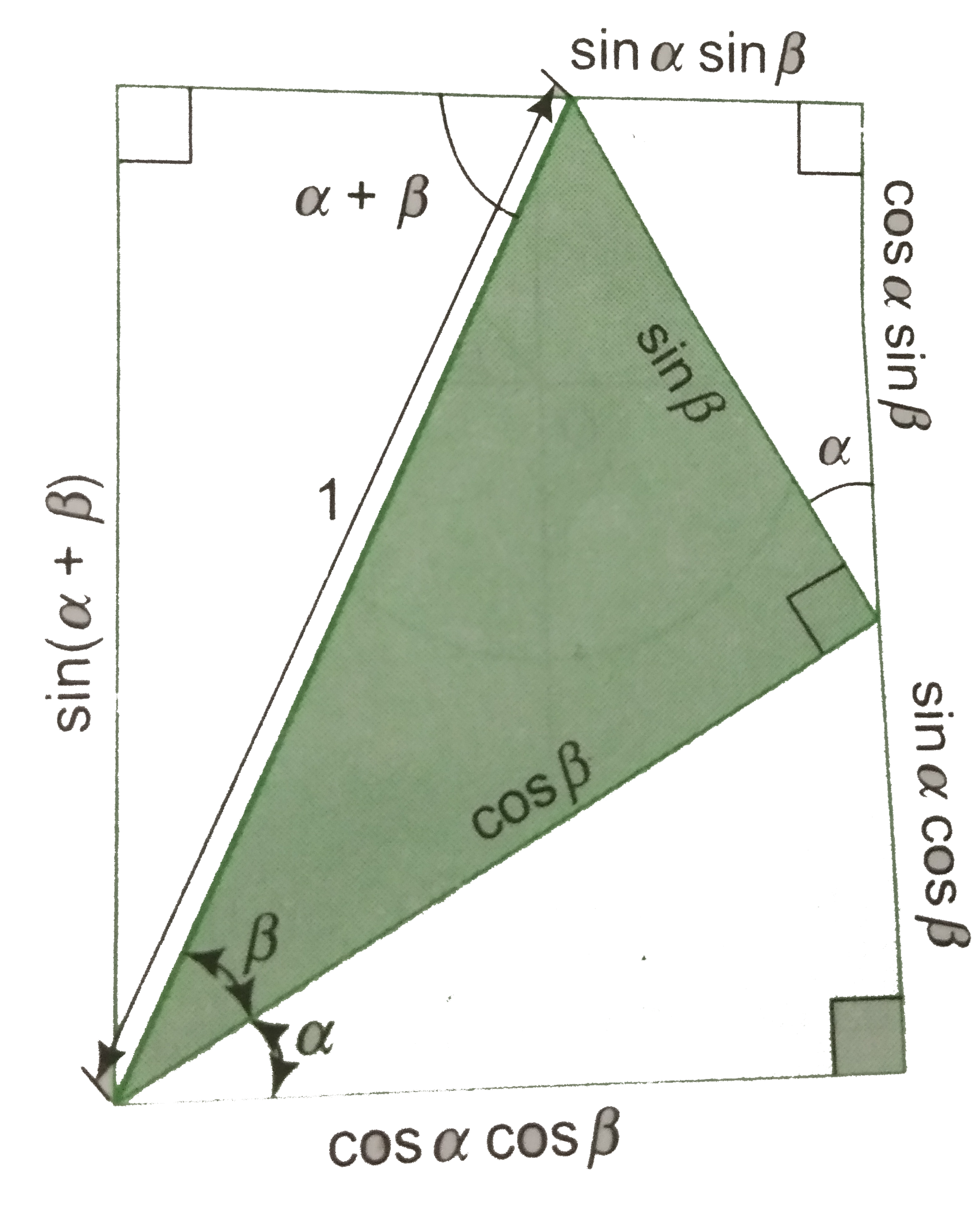
By geometrical interpretation, prove that
(i) sin(α+β)=sinαcosβ+sinβcosα
(ii) cos(α+β)=cosαcosβ−sinαsinβ
Text Solution
|
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.1
8 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.2
8 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
sinα+sinβ=a,cosα+cosβ=b⇒sin(α+β)
View SolutionIf sinα+sinβ=a,cosα+cosβ=b⇒sin(α+β)=
View Solutionf(α,β)=cos2(α)+cos2(α+β)−2cosαcosβcos(α+β) is
View SolutionShow by vector method that sin(α−β)=sinαcosβ−cosαsinβ.
View SolutionShow by vector method that sin(α−β)=sinαcosβ−cosαsinβ.
View SolutionShow that: sin2α+sin2β+2sinαsinβcos(α+β)=sin2(α+β)
View SolutionShow that: sin2α+sin2β+2sinαsinβcos(α+β)=sin2(α+β)
View SolutionIf cosα+cosβ=0=sinα+sinβ, then prove that cos2α+cos2β=−2cos(α+β).
View SolutionIf cosα+cosβ=0=sinα+sinβ, then prove that cos2α+cos2β=−2cos(α+β).
View SolutionProve that ∣∣ ∣ ∣∣cosαcosβcosαsinβsinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣=cos2α
View Solution