Calculate Karl Pearson's coefficient of correlation between x and y for the following data and interpret the result:
(1, 6), (2, 5), (3, 7), (4, 9), (5, 8), (6, 10), (7, 11), (8, 13), (9, 12).
To calculate Karl Pearson's coefficient of correlation (r) between the given data points, we will follow these steps:
Step 1: Calculate the means of x and y
Given the data points are:
- x: 1, 2, 3, 4, 5, 6, 7, 8, 9
- y: 6, 5, 7, 9, 8, 10, 11, 13, 12
Mean of x (x̄):
xˉ=1+2+3+4+5+6+7+8+99=459=5
Mean of y (ȳ):
ȳ = \frac{6 + 5 + 7 + 9 + 8 + 10 + 11 + 13 + 12}{9} = \frac{81}{9} = 9
Step 2: Calculate (x - x̄) and (y - ȳ)
Now we will compute the deviations from the mean for both x and y.
| x | y | x - x̄ | y - ȳ |
|---|---|--------|-------|
| 1 | 6 | -4 | -3 |
| 2 | 5 | -3 | -4 |
| 3 | 7 | -2 | -2 |
| 4 | 9 | -1 | 0 |
| 5 | 8 | 0 | -1 |
| 6 | 10| 1 | 1 |
| 7 | 11| 2 | 2 |
| 8 | 13| 3 | 4 |
| 9 | 12| 4 | 3 |
Step 3: Calculate (x - x̄)² and (y - ȳ)²
Next, we square the deviations.
| x - x̄ | (x - x̄)² | y - ȳ | (y - ȳ)² |
|--------|-----------|-------|----------|
| -4 | 16 | -3 | 9 |
| -3 | 9 | -4 | 16 |
| -2 | 4 | -2 | 4 |
| -1 | 1 | 0 | 0 |
| 0 | 0 | -1 | 1 |
| 1 | 1 | 1 | 1 |
| 2 | 4 | 2 | 4 |
| 3 | 9 | 4 | 16 |
| 4 | 16 | 3 | 9 |
Step 4: Calculate the sums
Now we will sum these values.
∑(x−xˉ)²=16+9+4+1+0+1+4+9+16=60
∑(y−ȳ)²=9+16+4+0+1+1+4+16+9=60
∑(x−xˉ)(y−ȳ)=(−4)(−3)+(−3)(−4)+(−2)(−2)+(−1)(0)+(0)(−1)+(1)(1)+(2)(2)+(3)(4)+(4)(3)
Calculating this gives:
12+12+4+0+0+1+4+12+12=57
Step 5: Calculate the coefficient of correlation (r)
Using the formula for Karl Pearson's coefficient of correlation:
r=∑(x−xˉ)(y−ȳ)√∑(x−xˉ)²⋅√∑(y−ȳ)²
Substituting the values we calculated:
r=57√60⋅√60=5760=0.95
Step 6: Interpretation of the result
The value of Karl Pearson's coefficient of correlation (r) is 0.95. This indicates a very strong positive correlation between the variables x and y. This means that as the values of x increase, the values of y also tend to increase significantly.
Given the data points are:
- x: 1, 2, 3, 4, 5, 6, 7, 8, 9
- y: 6, 5, 7, 9, 8, 10, 11, 13, 12
xˉ=1+2+3+4+5+6+7+8+99=459=5
ȳ = \frac{6 + 5 + 7 + 9 + 8 + 10 + 11 + 13 + 12}{9} = \frac{81}{9} = 9
Now we will compute the deviations from the mean for both x and y.
|---|---|--------|-------|
| 1 | 6 | -4 | -3 |
| 2 | 5 | -3 | -4 |
| 3 | 7 | -2 | -2 |
| 4 | 9 | -1 | 0 |
| 5 | 8 | 0 | -1 |
| 6 | 10| 1 | 1 |
| 7 | 11| 2 | 2 |
| 8 | 13| 3 | 4 |
| 9 | 12| 4 | 3 |
Next, we square the deviations.
|--------|-----------|-------|----------|
| -4 | 16 | -3 | 9 |
| -3 | 9 | -4 | 16 |
| -2 | 4 | -2 | 4 |
| -1 | 1 | 0 | 0 |
| 0 | 0 | -1 | 1 |
| 1 | 1 | 1 | 1 |
| 2 | 4 | 2 | 4 |
| 3 | 9 | 4 | 16 |
| 4 | 16 | 3 | 9 |
Now we will sum these values.
∑(y−ȳ)²=9+16+4+0+1+1+4+16+9=60
∑(x−xˉ)(y−ȳ)=(−4)(−3)+(−3)(−4)+(−2)(−2)+(−1)(0)+(0)(−1)+(1)(1)+(2)(2)+(3)(4)+(4)(3)
Calculating this gives:
12+12+4+0+0+1+4+12+12=57
Using the formula for Karl Pearson's coefficient of correlation:
r=∑(x−xˉ)(y−ȳ)√∑(x−xˉ)²⋅√∑(y−ȳ)²
Substituting the values we calculated:
r=57√60⋅√60=5760=0.95
The value of Karl Pearson's coefficient of correlation (r) is 0.95. This indicates a very strong positive correlation between the variables x and y. This means that as the values of x increase, the values of y also tend to increase significantly.
Topper's Solved these Questions
- MATHEMATICS-2016BOOK - ICSECHAPTER - MATHEMATICS-2016EXERCISE - SECTION-B
6 Videos
- MATHEMATICS-2016BOOK - ICSECHAPTER - MATHEMATICS-2016EXERCISE - SECTION-C
6 Videos
- MATHEMATICS-2015BOOK - ICSECHAPTER - MATHEMATICS-2015EXERCISE - SECTION-C
5 Videos
- MATHEMATICS-2020BOOK - ICSECHAPTER - MATHEMATICS-2020EXERCISE - SECTION C
8 Videos
Similar Questions
Knowledge Check
If cov(X,Y)=16.5,Var(X)=8.25 and Var(Y)=33, then Karl Pearson's coefficient of correlation between X and Y is
A12B23C34D1
Find the Karl Pearson's coefficient of correlation between x and y for the following data:
x1618212022262715y2225242625303314
View SolutionCaculate Karl Pearson 's coefficient of correlation between X and Y from the following data :

Assume 80 and 130 as the mean values for X and Y respectively .
View SolutionCalculate Karl Pearson's coefficient of correlation between the heights of husbands and wives based on the following data ( given in inches ) and interpret the result . Take assumed means of husbands and wives are 70 and 66 respectively .
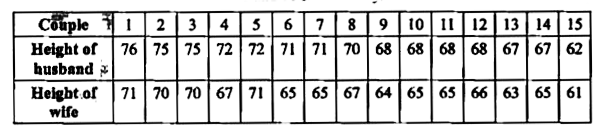
View SolutionArrange the following data as an array (descending order): (i) 2,0,3,4, 1, 2, 3,5
(ii) 9.1, 3.7, 5.6, 8.3, 11.5, 10.6
View SolutionIf f={(1,4),(2,5),(3,6)} and g={(4,8),(5,7),(6,9)}, then gof is
View SolutionFind the mean deviation about the median for the following data:
11, 3, 8, 7, 5, 14, 10, 2, 9
View SolutionFind the standard deviation for the following data: (i) x: , 3, 8, 13, 18, 23 f: , 7, 10, 15, 10, 6 (ii) x: , 2, 3, 4, 5, 6, 7, 7 f: , 4, 9, 16, 14, 11, 6, 6
View Solution


