Calculate the median from the following data: Marks: 0-10 10-30 30-60 60-80 80-90 No. of Students 5 15 30 8 2
To calculate the median from the given data, we will follow these steps:
Step 1: Create a Frequency Table
We will organize the data into a frequency table with cumulative frequencies.
| Marks Range | Frequency (f) | Cumulative Frequency (CF) |
|-------------|---------------|---------------------------|
| 0 - 10 | 5 | 5 |
| 10 - 30 | 15 | 20 |
| 30 - 60 | 30 | 50 |
| 60 - 80 | 8 | 58 |
| 80 - 90 | 2 | 60 |
Step 2: Calculate Total Frequency (n)
Now, we calculate the total number of students (n) by summing the frequencies.
n=5+15+30+8+2=60
Step 3: Find n/2
Next, we find n/2 to determine the median position.
n/2=60/2=30
Step 4: Identify the Median Class
We need to find the cumulative frequency just greater than or equal to n/2. From the cumulative frequency table, we see:
- CF for 0-10: 5
- CF for 10-30: 20
- CF for 30-60: 50 (this is the first cumulative frequency greater than 30)
Thus, the median class is 30 - 60.
Step 5: Identify L, F, f, and H
In the median class (30 - 60):
- L (lower boundary of median class) = 30
- F (cumulative frequency of the class before the median class) = 20
- f (frequency of the median class) = 30
- H (class width) = 60 - 30 = 30
Step 6: Apply the Median Formula
We use the median formula:
Median=L+(n/2−Ff)×H
Substituting the values:
Median=30+(30−2030)×30
Median=30+(1030)×30
Median=30+10
Median=40
Final Answer
The median of the given data is 40.
---
We will organize the data into a frequency table with cumulative frequencies.
|-------------|---------------|---------------------------|
| 0 - 10 | 5 | 5 |
| 10 - 30 | 15 | 20 |
| 30 - 60 | 30 | 50 |
| 60 - 80 | 8 | 58 |
| 80 - 90 | 2 | 60 |
Now, we calculate the total number of students (n) by summing the frequencies.
Next, we find n/2 to determine the median position.
We need to find the cumulative frequency just greater than or equal to n/2. From the cumulative frequency table, we see:
- CF for 10-30: 20
- CF for 30-60: 50 (this is the first cumulative frequency greater than 30)
In the median class (30 - 60):
- L (lower boundary of median class) = 30
- F (cumulative frequency of the class before the median class) = 20
- f (frequency of the median class) = 30
- H (class width) = 60 - 30 = 30
We use the median formula:
The median of the given data is 40.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the mode of the following data:
110,80,70,90, 120,90, 80,70,60,80A80B110C90D120
Calculate the median from the following distribution: Class: 5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45 Frequency: 5 6 15 10 5 4 2 2
View SolutionCaculate the median and mode from the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 2 18 30 45 35 20 6 3View SolutionFind the standard deviation for the following data:
10, 20, 30, 40, 50, 60, 70, 80, 90View SolutionFind the mean deviation about median for the following data
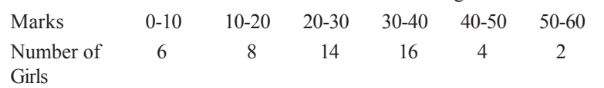 View Solution
View SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View SolutionCalculate the median deviation from the median of the following data: Wages per week (in Rs.), 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 No. of workers, 4, 6, 10, 20, 10, 6, 4
View SolutionFind the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547View Solution

