Doubtnut Promotions Sticky

Case Study-1: Consider a right triangle, where a and b are its length, and base and c is its hypotenuse as shown below. When we observe and apply the trigonometric functions to make a relationship between angles and sides of the right triangle. We can obtain the results as per the calculations and the table depicted below.
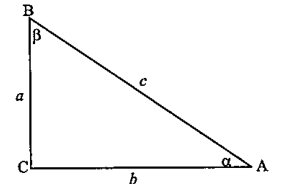
Case Study-1: Consider a right triangle, where a and b are its length, and base and c is its hypotenuse as shown below. When we observe and apply the trigonometric functions to make a relationship between angles and sides of the right triangle. We can obtain the results as per the calculations and the table depicted below. If the right angle of the right triangle ABC is at the point C, then the sine (sin), cosine (cos) and tangent (tan) of the angles alpha (at the point A) and beta (at the point B). It should be noted that sin alpha cos beta are the equal and same goes for sin alpha and cos beta. So, to find sine of the angle, we divided the side that is opposite of that angle and the hypotenuse. To find the cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse. Thus, Find the sum of cosalpha+cosbeta of right angled triangle, if the lengths a and b are increased twice of their original values.
If the right angle of the right triangle ABC is at the point C, then the sine (sin), cosine (cos) and tangent (tan) of the angles α (at the point A) and β (at the point B). It should be noted that sin α cos β are the equal and same goes for sin α and cos β. So, to find sine of the angle, we divided the side that is opposite of that angle and the hypotenuse. To find the cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse.
Thus,
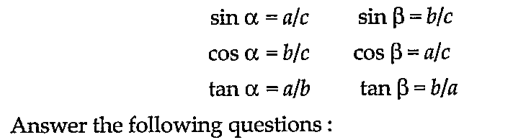
ocr_image
Find the sum of cosα+cosβ of right angled triangle, if the lengths a and b are increased twice of their original values.

A

5/7

B

5/6

C

3/5

D

7/5

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

|
Answer

Step by step video, text & image solution for Case Study-1: Consider a right triangle, where a and b are its length, and base and c is its hypotenuse as shown below. When we observe and apply the trigonometric functions to make a relationship between angles and sides of the right triangle. We can obtain the results as per the calculations and the table depicted below. If the right angle of the right triangle ABC is at the point C, then the sine (sin), cosine (cos) and tangent (tan) of the angles alpha (at the point A) and beta (at the point B). It should be noted that sin alpha cos beta are the equal and same goes for sin alpha and cos beta. So, to find sine of the angle, we divided the side that is opposite of that angle and the hypotenuse. To find the cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse. Thus, Find the sum of cosalpha+cosbeta of right angled triangle, if the lengths a and b are increased twice of their original values. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023
Class 10MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Base of a right angled triangle is

    A√(Hypotenous)2+(Perpendicular)2
    B√(Hypotenous)2−(Perpendicular)2
    C√(Perpendicular)2−(Hypotenous)2
    DNone of These
  • Question 2 - Select One

    If the length of sides of right angled triangle are in AP, then their ratio is

    A3:4:5
    B2:3:4
    C1:2:3
    Dnone of these
  • Question 3 - Select One

    In a right-angled triangle with sides a and b, hypotenuse c, the altitude drawn on the hypotenuse is x. Then

    Aab=x2
    B1a+1b=1x
    Ca2+b2=2x2
    D1a2+1b2=1x2