Case Study Based- 3
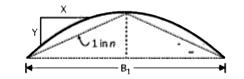
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
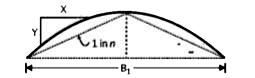
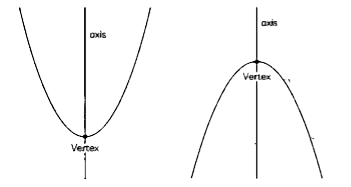
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is
x2−6x+2
x2−36
x2−6
x2−3
Step by step video & image solution for Case Study Based- 3 Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape. Parabola A parabola is the graph that results from p(x) = ax^(2)+bx+c Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex. The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART - B SECTION - III8videos
SAMPLE PAPER 01
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART - B SECTION - IV9videos
SAMPLE PAPER 01
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART-B (SECTION-V)4videos
SAMPLE PAPER 01
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -6 EXERCISE - Part - B (Section - V)6videos
SAMPLE PAPER -6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 02EXERCISE - SECTION - D9videos
SAMPLE PAPER 02
Similar Questions
Case Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
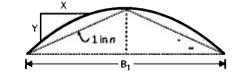
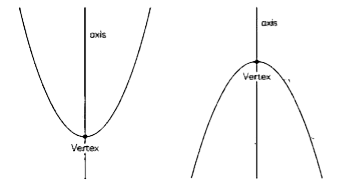
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
Graph of a quadratic polynomial is aView SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
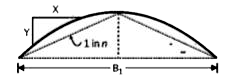
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
The number of zeroes that polynomial f(x)=(x−2)2+4 can have is:View SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
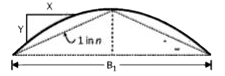
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
If the highway overpass is represented by x2−2x−8. Then its zeroes areView SolutionCase Study Based- 3
Applications of Parabolas-Highway Overpasses/Underpasses A highway underpass is parabolic in shape.

Parabola
A parabola is the graph that results from p(x)=ax2+bx+c
Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the Vertex.
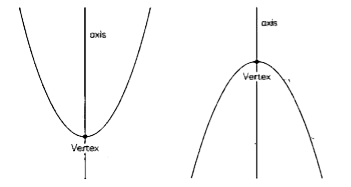
The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomialView SolutionWrite the axis of symmetry of the parabola y2=x.
View SolutionThe point on the axis of symmetry that bisects the parabola is called the "vertex”, and it is the point where the curvature is greatest.
View SolutionIs the parabola y2=4x symmetrical about x-axis ?
View SolutionParabolas having their vertices at the origin and foci on the x-axis.
View SolutionFind the equation of the parabola with vertex at the origin, passing throgh the point P(3,-4) and symmetric about the y-axis.
View SolutionThree normals from a point to the parabola y2=4ax meet the axis of the parabola in points whose abscissa are in A.P. Find the locus of the point.
View Solution

