Check whether h(x)=|1−x+|x|| is continious at origin.Solution in Malayalam
Step by step video & image solution for Check whether h(x)=abs(1-x+absx) is continious at origin. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
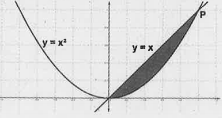
Consider the following figure
find the point of intersection (P) of the parabola and the line.
 04:03View Solution
04:03View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)03:45View SolutionFind values of 'x' so that log_(absx)abs(x-1)ge0 .
05:39View SolutionIf f(x)=abs(1/(abs(absx-2))+1/(abs(absx-3))) and g(x)=sin^(-1)(2sqrtx) , then f(x)=g(x) has
05:37View Solutiony=|x|என்ற வளைவரையின் மூலம் y=|x−1|+1 ஆகியவற்றை வரைக
04:20View Solutiony=|x|என்ற வளைவரையின் மூலம்y=|x+1|−1ஆகியவற்றை வரைக
02:54View SolutionEstablish that g(x)=1−x+|x| is continious at origin.
03:44View SolutionConsider the function f(x)=|x| , x∈R
Show that the function is continious at x=0.01:31View SolutionEvaluate: int_(-1)^1(absx+abs(x-1))dx
02:10View SolutionThe possible value of |x|+|x−1|=2 is :
01:19View SolutionIf f(x)=x√1−x2andg(x)=x√1+x2, then (fog)(x) =
05:40View SolutionWhat is the value of x if |x−1|+|x|=2:
06:58View SolutionSolve for x :
|x−1|+|x−2|+(x−3)≥603:29View SolutionSolution set of x satisfying ∣∣∣xx−1∣∣∣+|x|=x2|x−1| is
04:33View Solutionजाँच कीजिए कि द्विघात समीकरण 1x−2+2x−1=6x के मूल वास्तविक है अथवा नहीं। यदि हाँ, तो मूल ज्ञात कीजिए। (x≠0,1,2)
04:03View Solution

