Class Interval1−56−1011−1516−20Frequency3765
Consider the following statement is respect of the above frequency distribution.
I. The median is contained in the modal class.
II. The distribution is bell-shaped.
Which of the above statement is/are correct?
Only I
Only II
Both I and II
Neither I nor II
The correct Answer is:D
To solve the problem, we need to analyze the given frequency distribution and evaluate the two statements regarding the median and the shape of the distribution.
Step 1: Define the Class Intervals and Frequencies
The class intervals and their corresponding frequencies are as follows:
- Class Interval: 1-5, 6-10, 11-15, 16-20
- Frequency: 3, 7, 6, 5
Step 2: Adjust the Class Intervals
To make the class intervals continuous, we can adjust them by adding and subtracting 0.5:
- Adjusted Class Intervals:
- 0.5 to 5.5
- 5.5 to 10.5
- 10.5 to 15.5
- 15.5 to 20.5
Step 3: Calculate the Cumulative Frequency
Now, we calculate the cumulative frequency:
- For the first interval (0.5 to 5.5): 3
- For the second interval (5.5 to 10.5): 3 + 7 = 10
- For the third interval (10.5 to 15.5): 10 + 6 = 16
- For the fourth interval (15.5 to 20.5): 16 + 5 = 21
So, the cumulative frequencies are:
- 3, 10, 16, 21
Step 4: Calculate n and n/2
The total number of observations (n) is the sum of the frequencies:
- n = 3 + 7 + 6 + 5 = 21
Now, calculate n/2:
- n/2 = 21 / 2 = 10.5
Step 5: Identify the Median Class
To find the median class, we look for the cumulative frequency that is just greater than n/2 (10.5):
- The cumulative frequency just greater than 10.5 is 16, which corresponds to the class interval 10.5 to 15.5.
Step 6: Calculate the Median
Using the median formula:
Median=L+(n/2−CFf)×h
where:
- L = lower limit of the median class = 10.5
- CF = cumulative frequency of the class before the median class = 10
- f = frequency of the median class = 6
- h = width of the class interval = 5 (from 10.5 to 15.5)
Substituting the values:
Median=10.5+(10.5−106)×5
=10.5+(0.56)×5
=10.5+2.56
=10.5+0.4167≈10.917
Step 7: Evaluate the Statements
1. Statement I: The median is contained in the modal class.
- The modal class is the class with the highest frequency, which is 6-10 (frequency 7). The median (10.917) is not in this class. Therefore, this statement is false.
2. Statement II: The distribution is bell-shaped.
- To determine if the distribution is bell-shaped, we look at the cumulative frequency. The cumulative frequencies are increasing (3, 10, 16, 21), which does not form a bell shape. Therefore, this statement is also false.
Conclusion
Both statements are incorrect.
Final Answer
Neither statement I nor II is correct.
---
The class intervals and their corresponding frequencies are as follows:
- Class Interval: 1-5, 6-10, 11-15, 16-20
- Frequency: 3, 7, 6, 5
To make the class intervals continuous, we can adjust them by adding and subtracting 0.5:
- Adjusted Class Intervals:
- 0.5 to 5.5
- 5.5 to 10.5
- 10.5 to 15.5
- 15.5 to 20.5
Now, we calculate the cumulative frequency:
- For the first interval (0.5 to 5.5): 3
- For the second interval (5.5 to 10.5): 3 + 7 = 10
- For the third interval (10.5 to 15.5): 10 + 6 = 16
- For the fourth interval (15.5 to 20.5): 16 + 5 = 21
- 3, 10, 16, 21
The total number of observations (n) is the sum of the frequencies:
- n = 3 + 7 + 6 + 5 = 21
- n/2 = 21 / 2 = 10.5
To find the median class, we look for the cumulative frequency that is just greater than n/2 (10.5):
- The cumulative frequency just greater than 10.5 is 16, which corresponds to the class interval 10.5 to 15.5.
Using the median formula:
Median=L+(n/2−CFf)×h
where:
- L = lower limit of the median class = 10.5
- CF = cumulative frequency of the class before the median class = 10
- f = frequency of the median class = 6
- h = width of the class interval = 5 (from 10.5 to 15.5)
Median=10.5+(10.5−106)×5
=10.5+(0.56)×5
=10.5+2.56
=10.5+0.4167≈10.917
1. Statement I: The median is contained in the modal class.
- The modal class is the class with the highest frequency, which is 6-10 (frequency 7). The median (10.917) is not in this class. Therefore, this statement is false.
- To determine if the distribution is bell-shaped, we look at the cumulative frequency. The cumulative frequencies are increasing (3, 10, 16, 21), which does not form a bell shape. Therefore, this statement is also false.
Both statements are incorrect.
Neither statement I nor II is correct.
Topper's Solved these Questions
- BOOK - NDA PREVIOUS YEARSCHAPTER - SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM EXERCISE - MCQ271videos
SETS, RELATIONS, FUNCTIONS AND NUMBER SYSTEM
- BOOK - NDA PREVIOUS YEARSCHAPTER - TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONSEXERCISE - MCQ238videos
TRIGONOMETRY - RATIO & IDENTITY , TRIGONOMETRIC EQUATIONS
Similar Questions
The age distribution of 40 children is as follows:

Consider the following statements in respect of the above frequency distribution:
1. The median of the age distribution is 7 years.
2. 70% of the children are in the age group 6-9 years.
3. The modal age of the children is 8 years.
Which of the above statements are correct?View SolutionThe age distribution of 40 children is as follows:

Consider the following statements in respect of the above frequency distribution:
1. The median of the age distribution is 7 years.
2. 70% of the children are in the age group 6-9 years.
3. The modal age of the children is 8 years.
Which of the above statements are correct?View Solution
Knowledge Check
- Question 1 - Select One
Consider the following statements in respect of class intervals of grouped frequency distribution:
1. Class intervals need out be mutually exclusive.
2. Class intervals should be exhaustive.
3. Class intervals need not be of equal width.
Which of the above statements are correct?A1 and 2 onlyB2 and 3 onlyC1 and 3 onlyD1, 2 and 3 - Question 2 - Select One
Consider the following statements in respect of class intervals of grouped frequency distribution.
1 Class intervals need not be mutually exclusive.
2.Class intervals should be exhaustive
3.Class intervals need not be of equal width Which of the above statements are correctABoth 1 and 2BBoth 2 and 3CBoth 1 and 3D1, 2 and 3 - Question 3 - Select One
Class Interval0.1010−2020−3030−4040−50Frequency5020510
What is the median of the above frequency distribution?A23B24C25D26
Consider the following statements :
1. A frequency distribution condenses the data and reveals its important features.
2. A frequency distribution is an equivalent representation of original data.
Which of the above statements is/are correct ?View SolutionFor the following raw data prepare a frequency distribution with a class interval of 5 on inclusive basis :
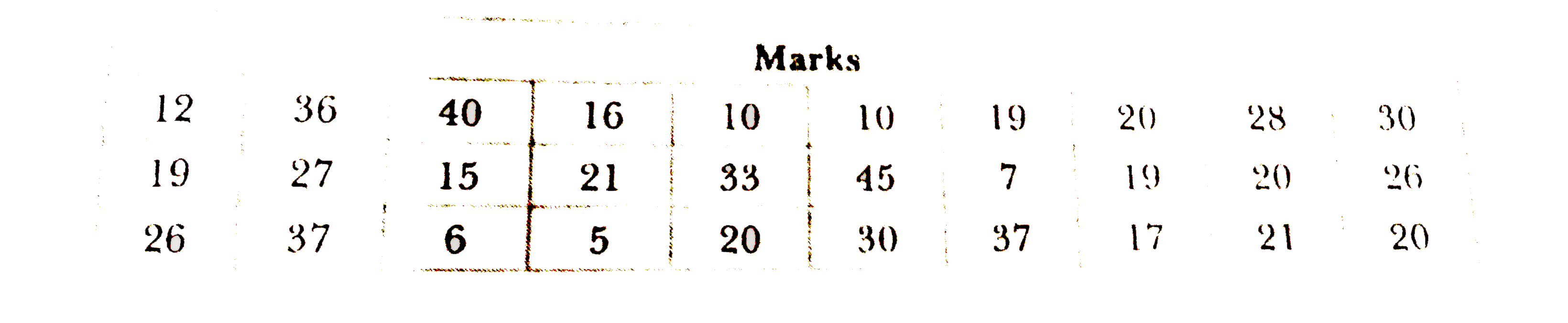 View Solution
View SolutionClass Interval0.1010−2020−3030−4040−50Frequency5020510
What is the mean of the above frequency distribution?View SolutionConsider the following statements in respect of histogram :
1. Histogram is an equivalent graphical representation of the frequency distribution.
2. Histogram is suitable for continuous random variables, where the total frequency of an interval is evenly distributed over the interval.
What of the statements given above is/are correct?View SolutionConsider the following statements in respect of histogram :
1. The histogram is a suitable representation of a frequency distribution of a continuous variable.
2. The area included under the whole histogram is the total frequency.
Which of the above statements is/are correct?View Solution

